Apprendre Maple Tableau des variations
 
  Page d'accueilPage d'accueil   RechercherRechercher   Forum de discussionForum de discussion   ContactContact   SommaireSommaire 
  Cours MapleCours Maple   Travaux dirigésTravaux dirigés   Thèmes d'activitésThèmes d'activités   MapletsMaplets 
Ecran MapleEcran Maple  TéléchargementTéléchargement  BibliographieBibliographie  LiensLiens  

 

Page d'accueil   Maplets   << Page précédente   Page suivante >>


 

Graphe et tableau de variations d'une fonction f
© Alain Le Stang - "Apprendre Maple" - 2004
Sélectionner Edit/Execute/Worksheet ou cliquer le bouton !!! pour exécuter ce Maplet.
 

> restart:
with(Maplets[Elements]): with(plots):

Warning, the name changecoords has been redefined
 

> tab_var:=proc(f,x::name,fonc::name,a,b)
global liste;
local liste_X,signe_derivee,liste_def,texte,fleche,traits_verticaux,
N,X,Y,S,Lf,largeur,hauteur,bordures,doubles_traits,fleches,limites,colonne1,ligne1,signes,h,i,l,w;

#########################################################
####                                                 procédure liste_X                                                     ####
#########################################################
liste_X:=proc(f,x::name,a,b)
local i,j,DF,F,L,M,N,S;
L:={a,b};
F:=[singular(f(x))]:
for i to nops(F) do
 L:=L union {rhs(op(F[i]))}
end do;
DF:=[singular(D(f)(x))]:
for i to nops(DF) do
 L:=L union {rhs(op(DF[i]))}
end do;
S:=[solve(D(f)(x),x)]:
if S=[x] then S:=[a,b] end if;
for i to nops(S) do
 L:=L union {S[i]}
end do;
L:=sort(convert(L,list));
M:=NULL;
for i to nops(L) do
 if evalb(evalf(L[i])>=evalf(a) and evalf(L[i])<=evalf(b)) then M:=M,L[i] end if
end do;
M:=sort(map(evalf,convert({M},list))):
N:=NULL;
for i to nops(M) do
 for j to nops(L) do
    if evalb(evalf(L[j])=M[i]) then N:=N,L[j] end if;
 end do;
end do;
[N]
end proc:

#########################################################
####                                           procédure signe_derivee                                              ####
#########################################################
signe_derivee:=proc(f,L::list,X::list)
local i,j,M,s;
M:=NULL;
for i to nops(X)-1 do
  if X[i]=-infinity then
      s:=evalf(simplify(D(f)(X[i+1]-1)))
  elif X[i+1]=infinity then
      s:=evalf(simplify(D(f)(X[i]+1)))
  else s:=evalf(simplify(D(f)((X[i]+X[i+1])/2)))
  end if;
  if s=0 then M:=M,0 else M:=M,sign(s) end if;
end do;
M:=[M]:
for i from nops(M) to 2 by -1 do
 if sign(M[i-1])=sign(M[i]) then
   if L[i][2]=true then M[i-1]:=M[i-1]+M[i] end if
 end if;
end do;
for i to nops(M) do
 if is(M[i],integer) and abs(M[i])>1 then
   for j from i+1 to i+abs(M[i])-1 do
      if M[i]>0 then M[j]:=evalf((j-i)/(abs(M[i])),2)
      else M[j]:=-(1+evalf((j-i)/M[i],2)) end if;  
   end do
 end if;
end do;
M
end proc:

#########################################################
####                                               procédure list_def                                                      ####
#########################################################
liste_def:=proc(f,L::list)
local i,M,N,b,c;
M:=NULL:
for i in L do
 b:=true;c:=true;N:=NULL:
 try
    simplify(f(i));
 catch:
    b:=false;
 end try;
 N:=N,i,b;
 try
    simplify(D(f)(i));
 catch:
    c:=false;
 end try;
 N:=N,c;
 M:=M,[N]
end do;
[M];
end proc:

#########################################################
####                                                       procédure texte                                                  ####
#########################################################
texte:=proc(absc,ord,txt,police,taille,drapeau,indice)
if txt=-infinity then
  textplot([absc,ord,"-"],font=[police,taille]),textplot([absc+1.2,ord,"¥"],font=[SYMBOL,taille])
elif txt=infinity then
  textplot([absc,ord,"+¥"],font=[SYMBOL,taille])
elif drapeau=0 then
  textplot([absc,ord,txt],font=[police,taille])
else
  if is(txt,rational) then  
    textplot([absc,ord,txt],font=[police,taille])
  else  
    textplot([absc,ord,cat(drapeau,indice)],font=[police,taille])
  end if;
end if;
end proc:

#########################################################
####                                                     procédure fleche                                                   ####
#########################################################
fleche:=proc(P1,P2)
local fl;

fl:=proc(x1,y1,x2,y2,a)
local d,x3,y3,x4,y4,x5,y5;
d:=evalf(sqrt((x2-x1)^2+(y2-y1)^2)):
x3:=evalf(x1+(d-a)/d*(x2-x1)):y3:=evalf(y1+(d-a)/d*(y2-y1)):
x4:=evalf(x2+0.5*(sqrt(3)*(x3-x2)-y3+y2)):
y4:=evalf(y2+0.5*(x3-x2+sqrt(3)*(y3-y2))):
x5:=evalf(x2+0.5*(sqrt(3)*(x3-x2)+y3-y2)):
y5:=evalf(y2+0.5*(-x3+x2+sqrt(3)*(y3-y2))):
plot([[x1,y1],[x2,y2],[x4,y4],[x2,y2],[x5,y5]],color=black)
end proc:

fl(P1[1],P1[2],P1[1]+P2[1],P1[2]+P2[2],1.5)
end proc:

#########################################################
####                                                       procédure principale                                           ####
#########################################################
X:=liste_X(f,x,a,b):  #print(`liste_X `=X):
Lf:=liste_def(f,X):   #print(`liste_def `=Lf):
S:=signe_derivee(f,Lf,X): #print(`signe_derivee `=S):

largeur:=10:hauteur:=5:
w:=nops(X)*largeur:

# affichage des bordures du tableau
bordures:=[
plot([[0,0],[w,0],[w,4*hauteur],[0,4*hauteur],[0,0],[0.9*largeur,0],[0.9*largeur,4*hauteur]],color=black),
plot([[0,3*hauteur],[w,3*hauteur]],color=black),plot([[0,2*hauteur],[w,2*hauteur]],color=black)]:

# affichage des traits verticaux de séparation
traits_verticaux:=NULL:
for i to nops(S) do
 if is(S[i],integer) then
traits_verticaux:=traits_verticaux,plot([[(i+abs(S[i]))*largeur,0],[(i+abs(S[i]))*largeur,3*hauteur]],color=black)
 end if;
end do;
traits_verticaux:=[traits_verticaux]:

# affichage des doubles traits verticaux aux points où f (resp. f') n'est pas définie
doubles_traits:=NULL:
for i to nops(Lf) do
 if i=1 then l:=largeur*0.925 else l:=largeur end if;
 if Lf[i][2]=false then
    doubles_traits:=doubles_traits,plot([[i*l+0.6,0],[i*l+0.6,2*hauteur]],color=black)
 end if;
 if Lf[i][3]=false then         doubles_traits:=doubles_traits,plot([[i*l+0.6,2*hauteur],[i*l+0.6,3*hauteur]],color=black)
 else
    if simplify(D(f)(Lf[i][1]))=0 and abs(Lf[i][1])<>infinity then     doubles_traits:=doubles_traits,texte(l*i,2*hauteur+hauteur/2,0,HELVETICA,10,0,0),
plot([[l*i,2*hauteur],[l*i,3*hauteur]],color=black)    
    end if
 end if
end do;
doubles_traits:=[doubles_traits]:

# affichage des textes dans la première colonne : "x" , "f(x)" , "f'(x)"  
colonne1:=[texte(0.45*largeur,3*hauteur+hauteur/2,x,HELVETICA,10,0,0),
        texte(0.45*largeur,2*hauteur+hauteur/2,cat(fonc,"`(",x,")"),HELVETICA,10,0,0),
        texte(0.45*largeur,hauteur,cat(fonc,`(`,x,`)`),HELVETICA,10,0,0)]:

# affichage des valeurs de x dans la première ligne du tableau
ligne1:=NULL:
for i to nops(X) do
 if X[i]=-infinity then ligne1:=ligne1,texte(largeur/20+largeur,3*hauteur+hauteur/2,X[i],HELVETICA,10,0,0)
 elif X[i]=infinity then ligne1:=ligne1,texte(w-largeur/4,3*hauteur+hauteur/2,X[i],SYMBOL,10,0,0)
 else
    ligne1:=ligne1,texte(largeur*i,3*hauteur+hauteur/2,X[i],HELVETICA,10,x,i)
 end if
end do:
ligne1:=[ligne1]:

# affichage des signes de la dérivée dans la seconde ligne et
# affichage des flèches associées dans la troisième ligne
signes:=NULL:fleches:=NULL:
for i to nops(S) do
  if S[i]<0 then
    signes:=signes,texte(largeur/2+largeur*i,2*hauteur+hauteur/2,"-",HELVETICA,10,0,0):  
    if is(S[i],integer) then fleches:=fleches,fleche([largeur*i+largeur/4,2*hauteur-hauteur/4],
[largeur*(abs(S[i])-1)+largeur/2,-2*hauteur+hauteur/2] )
    end if;
 elif S[i]=0 then
    signes:=signes,texte(largeur/2+largeur*i,2*hauteur+hauteur/2,"0",HELVETICA,10,0,0):    
fleches:=fleches,fleche([largeur*i+largeur/4,hauteur],[largeur*(abs(S[i])-1)+largeur/2,0] )  
 else
    signes:=signes,texte(largeur/2+largeur*i,2*hauteur+hauteur/2,"+",HELVETICA,10,0,0):
    if is(S[i],integer) then
fleches:=fleches,fleche([largeur*i+largeur/4,hauteur/4],[largeur*(abs(S[i])-1)+largeur/2,2*hauteur-hauteur/2] )
    end if;
 end if;
end do;
signes:=[signes]:
fleches:=[fleches]:

# détermination des valeurs de f(x) ou des limites (à gauche ou à droite)
Y:=NULL:
for i to nops(Lf) do
 if i=1 then
   Y:=Y,[simplify(limit(f(x),x=Lf[i][1],right))]
 elif i=nops(Lf) then
   Y:=Y,[simplify(limit(f(x),x=Lf[i][1],left))]
 else
   if Lf[i][2]=true then Y:=Y,[simplify(limit(f(x),x=Lf[i][1]))]
   else Y:=Y,[simplify(limit(f(x),x=Lf[i][1],left)),simplify(limit(f(x),x=Lf[i][1],right))]
   end if
 end if;
end do;
Y:=[Y]:  

# affichage des valeurs de f(x) ou des limites aux extrémités des flèches
limites:=NULL:
for i to nops(Y) do
if i=1 then
    if S[i]<0 then
     limites:=limites,texte(largeur+largeur/8,2*hauteur-hauteur/8,Y[i][1],HELVETICA,10,fonc,i)
    else    
     limites:=limites,texte(largeur+largeur/8,hauteur/4,Y[i][1],HELVETICA,10,fonc,i);
    end if;
elif i=nops(Y) then
    if S[i-1]<0 then
      limites:=limites,texte(i*largeur-1.8,hauteur/4,Y[i][1],HELVETICA,10,fonc,i)
    else                  
      limites:=limites,texte(i*largeur-1.8,2*hauteur-hauteur/8,Y[i][1],HELVETICA,10,fonc,i)
    end if;
else
if nops(Y[i])=2 then
     if S[i-1]<0 then
         limites:=limites,texte(i*largeur-1.8,hauteur/4,Y[i][1],HELVETICA,10,fonc,i)
     else
         limites:=limites,texte(i*largeur-1.8,2*hauteur-hauteur/8,Y[i][1],HELVETICA,10,fonc,i)
     end if;
     if S[i]<0 then
         limites:=limites,texte(i*largeur+1.8,2*hauteur-hauteur/8,Y[i][2],HELVETICA,10,fonc,i)
     else
         limites:=limites,texte(i*largeur+1.8,hauteur/4,Y[i][2],HELVETICA,10,fonc,i)
     end if;

else # nops(Y[i])=1
  if S[i]<0 then
     if is(S[i],integer) then h:=2*hauteur-hauteur/8 else h:=-2*hauteur*S[i] end if;
  end if;  
  if S[i]>0 then
     if is(S[i],integer) then h:=hauteur/4 else h:=2*hauteur*S[i] end if;
  end if;
  limites:=limites,texte(i*largeur,h,Y[i][1],HELVETICA,10,fonc,i)  
end if;
end if;
end do:
limites:=[limites]:

# valeurs particulières de x et des images f(x):
for i to nops(Y) do
 if nops(Y[i])=1 then Y[i]:=op(Y[i]) end if
end do;
liste:=[seq(x||i=Lf[i][1],i=1..nops(Lf)),seq(fonc||i=Y[i],i=1..nops(Y))]:
# tracé du tableau des variations de f
display(bordures,traits_verticaux,doubles_traits,colonne1,ligne1,signes,fleches,limites,axes=none,
scaling=unconstrained)
end proc:
 
   

 

> tab_var(t->1/(t^2-5*t+4)*sqrt(t+1),t,y,-1,infinity);op(liste);

[Plot]

t1 = -1, t2 = 1, t3 = 7/3, t4 = 4, t5 = infinity, y1 = 0, y2 = [infinity, -infinity], y3 = -3/20*30^(1/2), y4 = [-infinity, infinity], y5 = 0

> exemples:=[ [1/(t^2-5*t+4)*sqrt(t+1),t,f,-1,infinity,-1.5,10,-10,10],
[(x^2+1)/(2*x^2+x-4),x,g,-infinity,infinity,-10,10,-5,5],
[-x^4+2*x^3+3*x^2-4*x+5,x,h,-infinity,infinity,-5,5,-10,10], [exp(-u)/(u^2-1),u,i,-infinity,infinity,-5,2,-20,20],
[2*t/(t^2-4)+1/2*ln(abs((2+t)/(2-t))),t,j,-infinity,infinity,-10,10,-10,10] ]:

 
> MajExemples:=proc()
global exemples;
local v,ex;
v:=Maplets:-Tools:-Get('DDB'('value')):
if v="Ex1" then ex:=exemples[1]
elif v="Ex2" then ex:=exemples[2]
elif v="Ex3" then ex:=exemples[3]
elif v="Ex4" then ex:=exemples[4]
else ex:=exemples[5]
end if;
EffacerCourbe(); EffacerTabVar();
Maplets:-Tools:-Set('ExpFonc'('value')=ex[1]):  
Maplets:-Tools:-Set('NomVar'('value')=ex[2]):
Maplets:-Tools:-Set('NomFonc'('value')=ex[3]):
Maplets:-Tools:-Set('XVmin'('value')=ex[4]):
Maplets:-Tools:-Set('XVmax'('value')=ex[5]):
Maplets:-Tools:-Set('Xmin'('value')=ex[6]):
Maplets:-Tools:-Set('Xmax'('value')=ex[7]):
Maplets:-Tools:-Set('Ymin'('value')=ex[8]):
Maplets:-Tools:-Set('Ymax'('value')=ex[9]):
end proc:
 

 

> TabVarMaplet := Maplet( Window( 'title'="Graphe et tableau de variations",
BoxRow('vscroll'='always',
BoxRow(border=false, inset=0,
 [ BoxColumn(border=true, inset=0, 'caption'="Fonction",
      [TextField['NomFonc']("f",width=2), "de la variable", TextField['NomVar']("x",width=2),"Exemples:",DropDownBox['DDB']("Ex1",[Ex1,Ex2,Ex3,Ex4,Ex5],
 'onchange'='majEx')],
      [ TextField['ExpFonc'](),Button("Effacer",'onclick'='effFonc') ]
   ),
   BoxColumn(border=true, inset=0, 'caption'="Graphe",
      ["Pour les abscisses entre:",
      TextField['Xmin'](width=5), "et", TextField['Xmax'](width=5)],
      ["Pour les ordonnées entre:",
      TextField['Ymin'](value="-10",enabled=true,width=5),"et",
      TextField['Ymax'](value="10",enabled=true,width=5)],
      Plotter['PL1'](width=300,height=315),
      [Button("Effacer", 'onclick'='effCourbe'),
    Button['B1']("Représenter",  Action(
    Evaluate( 'PL1' = 'plot(ExpFonc,NomVar=Xmin..Xmax,discont=true,view=[Xmin..Xmax,Ymin..Ymax])' )
    )
    )]   
   ),
  [Button("Aide", RunDialog('MD1')), Button("Quitter", Shutdown())]
 ]
),

[ BoxColumn(border=true, inset=0, 'caption'="Variations",
       ["Pour les abscisses entre:",
       TextField['XVmin'](width=5),"et",TextField['XVmax'](width=5)],
       Plotter['PL2'](width=300,height=200),
       MathMLViewer['MMLV'](width=300,height=200),
       [Button("Effacer", 'onclick'='effTabVar'),
 Button['B2']("Tableau de variations",  Action(
 Evaluate( 'PL2' = 'tab_var(unapply(ExpFonc,NomVar),NomVar,NomFonc,XVmin,XVmax)'),
 Evaluate( 'MMLV' = 'MathML[Export](liste)')
 ))]     
 )
]
)),

MessageDialog['MD1']( "          © Alain Le Stang - ""Apprendre Maple"" - 2004\n\nCe maplet donne la représentation
graphique d'une fonction\n    et permet de visualiser son tableau de variations.", 'type'='information' ),


Action['effFonc'](
SetOption('NomFonc'="f"), SetOption('NomVar'="x"),
SetOption('ExpFonc'=""), SetOption('DDB'="Ex1")
),
Action['effCourbe'](
SetOption('Xmax'=""), SetOption('Ymax'="10"), SetOption('Xmin'=""), SetOption('Ymin'="-10"),
Evaluate( 'PL1' = 'plot(undefined,x=-10..10,axes=NONE)')
),
Action['effTabVar'](
SetOption('XVmax'=""), SetOption('XVmin'=""), SetOption('MMLV'=""),
Evaluate( 'PL2' = 'plot(undefined,x=-10..10,axes=NONE)' )
),
Action['majEx'](
),
Action['majEx'](
Evaluate('function'="MajExemples"),
Evaluate( 'PL1' = 'plot(ExpFonc,NomVar=Xmin..Xmax,discont=true,view=[Xmin..Xmax,Ymin..Ymax])' ),   
Evaluate( 'PL2' = 'tab_var(unapply(ExpFonc,NomVar),NomVar,NomFonc,XVmin,XVmax)'),
Evaluate( 'MMLV' = 'MathML[Export](liste)')
)
):
 
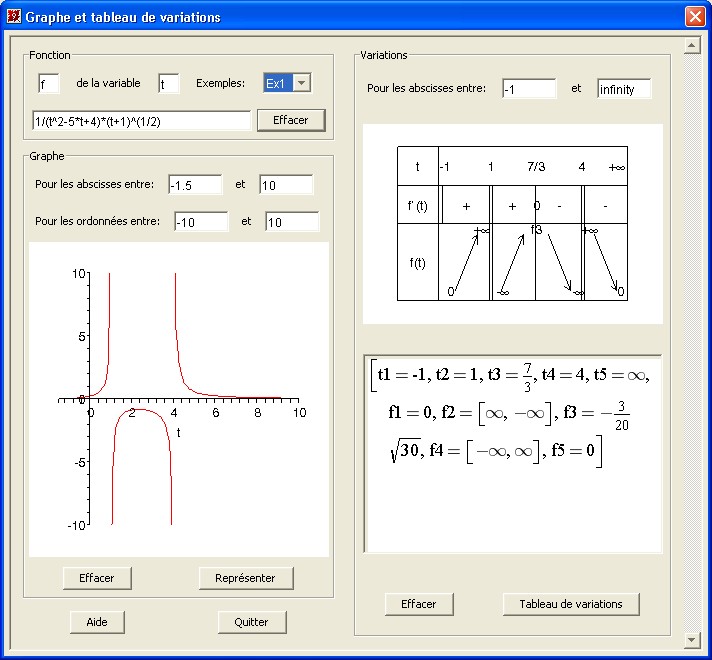
> Maplets[Display](TabVarMaplet);


 
 

 

 

haut de cette page


©  - Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.