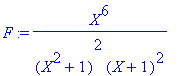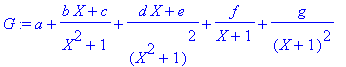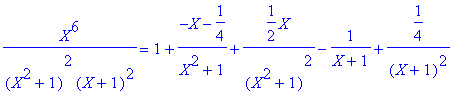|
Travail
dirigé 5 Polynômes et fractions rationnelles |
|
Page d'accueil Travaux dirigés << TD précédent TD suivant >> TD 5.1: Corrigé TD 5.1
1° La décomposition de F en éléments simples dans R s'écrit:
On réduit les fractions composant G au même dénominateur et on identifie les numérateurs de F et de G . En déduire les valeurs de a,b,c,d,e,f,g .
2° Calculer la décomposition de F en éléments simples dans C
TD 5.2:
L'algorithme de Hörner permet d'écrire P( x ) sous la forme :
Exemple:
Ecrire une procédure PolyHorner(P , x ) permettant d'écrire P( x ) sous cette forme , P étant un polynôme donné de K[ x ] , x étant le nom de la variable .
NB: il est interdit d'utiliser la fonction horner de MAPLE .
Grace à la fonction
cost
, évaluer le coût en opérations nécessaires pour évaluer Q et
Corrigé du Travail dirigé 5:
TD 5.1:
Question 1: > F:=X^6/(X^2+1)^2/(X+1)^2;
> G:=a+(b*X+c)/(X^2+1)+(d*X+e)/(X^2+1)^2+f/(X+1)+g/(X+1)^2;
> N:=convert(numer(G),polynom)-X^6:collect(N,X);
> solve({seq(coeff(N,X,k),k=0..degree(N))},{a,b,c,d,e,f,g});
> assign(%);F=G;
Question 2: > F=convert(F,parfrac,X,I);
TD 5.2:
>
PolyHorner:=proc(P::polynom,x::name)
> Q:=3*x^4+2*x^3-x^2+2*x+1;PolyHorner(Q,x);
> with(codegen,cost):cost(Q);cost(PolyHorner(Q,x));
|
© - Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.
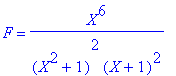
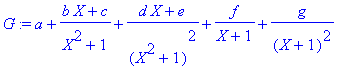
![P(x) = Sum(a[k]*x^k,k = 0 .. n)](images/td53.gif)