 |
Travail
dirigé 7 Maple en analyse |
|
Page d'accueil Travaux dirigés << TD précédent TD suivant >> TD 7:
1° Etablir les singularités de la fonction f et vérifier sa continuité.
2° Etudier les limites de f aux bornes des intervalles composant Df. Quelle est l'asymptote de la courbe Cf de f ?
3° Calculer f '( x ) et étudier son signe ( on aura recours à une fonction auxiliaire g ).
4° Représenter la courbe Cf.
5° Etudier la dérivabilité du prolongement par continuité de f aux points 0 et 1.
Corrigé du Travail dirigé 7: > f:=x->x^(x/(1-x));
> singular(f(x)); # D=IR+*\{1}
> iscont(f(x),x=0..1),iscont(f(x),x=1..infinity);
Conclusion: f est définie et continue sur ]0,1[ et ]1,+infini[.
> Limit(f(x),x=0,right)=limit(f(x),x=0,right);
> Limit(f(x),x=1,left)=limit(f(x),x=1,left);
> Limit(f(x),x=1,right)=limit(f(x),x=1,right);
> Limit(f(x),x=infinity)=limit(f(x),x=infinity);
Donc une asymptote, l'axe des abscisses, au voisinage de +infini.
> df:=normal(diff(f(x),x));
df=f ' a donc le signe de
> g:=x->ln(x)+1-x;
> solve(g(x)=0);
> solve(g(x)<0);
> solve(g(x)>0); # pas de solution g(x) est donc toujours négative et nulle pour x=1 . f est donc décroissante sur ]0,1[ et ]1,+infini[.
> plot(f(x),x=0..10,numpoints=1000,color=black);
Complément: f est prolongeable par continuité au point 0 puisque sa limite en ce point vaut 1. Cherchons si le prolongement obtenu est dérivable au point 0 en calculant: > Limit((f(x)-1)/x,x=0,right)=limit((f(x)-1)/x,x=0,right);
Le prolongement de f n'est pas dérivable au point 0. La limite de l'accroissement de f étant infinie,existence d'une tangente dirigée par Oy au point (0,1).
f est prolongeable par continuité au point 1 puisque sa limite en ce point vaut
Cherchons si le prolongement obtenu est dérivable au point 0 en calculant: > Limit((f(x)-exp(-1))/(x-1),x=1)=limit((f(x)-exp(-1))/(x-1),x=1);
Le prolongement de f est donc dérivable au point 1 et f '(1)=
C'est la pente de la tangente à Cf au point (1,
|
© - Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.
 .
.



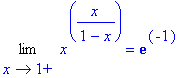
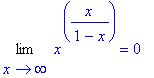

![[Maple Plot]](images/td714.gif)


 .
.