|
Page d'accueil
Thèmes d'activités
<< Thème précédent
Thème suivant >>
Compression de données: codage de Huffman
Le codage de Huffman
est une méthode non destructive de compression de données, c'est à dire qu'il n'y aura aucune perte lorsqu'on
reconstituera les données initiales à partir des données codées compressées. Dans cette feuille de calcul, nous coderons un texte défini à partir d'une chaîne de caractères ( Exemple 1 ), ou défini à partir d'un fichier
texte ( Exemple 2 ). L'unité élémentaire utilisée pour le codage d'informations sera le bit , ayant pour valeur 0 ou 1, chiffres de la numération binaire (base 2) Un octet (ou byte en anglais) est une suite de 8 bits , représentable par un entier de 0 à 255 en numération décimale (base 10), ou par
un entier de 0 à FF en numération hexadécimale (base 16).
Principe du codage de Huffman:
Fréquences d'apparition: L'algorithme de Huffman permet un codage de longueur variable, les caractères les plus fréquents étant représentés par des mots de
code courts.
Exemple 1 Considérons par exemple le texte source suivant à compresser:
|
> |
texte_source:="abcdcefaaeeeeeedaeaceaecefcebdcaeeaeebefecefecaedeabeccaeebeaecededeaaebaefefeeaebcea
daeaefeaececeea": |
texte_source contient 21 fois le caractère a , 7 fois les caractères b , d , f , 14 fois le caractère c et 44 fois le caractère e .
Au total, il y a 100 caractères dans texte_source .
Le tableau suivant montre la fréquence d'apparition de chaque caractère, son codage ASCII (par exemple a est codée 97 = 2^6+2^5+2^0,
soit 01100001 en base 2), et le codage qu'il aura après application de l'algorithme de Huffman.
On voit ici que le caractère le plus fréquent e sera représenté sur un bit par le code 0, alors qu'un caractère plus rare comme b sera
représenté par un code sur 4 bits: 1100. ![[Maple OLE 2.0 Object]](images/huffman1.gif) La procédure frequences construit une liste d'éléments de type [ caractère , fréquence ] , où caractère est l'une des lettres extraites du texte texte_source à compresser, et fréquence
est la fréquence d'apparition de ce caractère (la liste est triée dans l'ordre alphabétique des caractères):
|
> |
frequences:=proc(S::string)
local i,j,T,L,n,min,tmp;
n:=0:
for i to length(S) do
if not is(T[S[i]],posint) then n:=n+1: T[S[i]]:=1 else T[S[i]]:=T[S[i]]+1 end if
end do;
L:=NULL;
for i to n do
L:=L,[op(indices(T)[i]),op(entries(T)[i])]
end do:
L:=[L];
for j from n to 2 by -1 do
for i to j-1 do
if L[i][1]>L[i+1][1] then L:=subsop(i=L[i+1],i+1=L[i],L) end if
end do;
end do;
L
end proc:
|
|
> |
F:=frequences(texte_source);
|
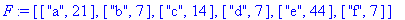
Arbre de Huffman:
Afin de coder les caractères, nous allons construire un arbre binaire .
L' arbre de Huffman ci-dessous est celui que nous devons construire à partir des données de l'exemple précédent:
![[Maple Bitmap]](images/huffman3.gif)
Un arbre est constitué de nœuds (représentés ici par des rectangles gris), et de feuilles (représentées ici par des rectangles verts). On appelle racine le nœud qui est le père de tous les nœuds (ici étiqueté noeud5). Un nœud donne naissance à deux descendants: un fils gauche et un fils droite , qui peuvent être des nœuds ou des feuilles.
Une feuille est un nœud qui n'a pas de fils. Nous constatons que le code attribué par Huffman à un caractère n'est autre que le code du chemin menant de la racine à la feuille
associée à ce caractère. Le code 1 signifie un déplacement vers le nœud fils gauche tandis que le code 0 signifie un déplacement vers le nœud fils droite.
Par exemple, pour accéder au caractère d , on doit parcourir successivement les branches codées 1 , 1,0,1 donc le code de d sera 1101.
Définition et opérations sur les arbres:
Définition: Pour représenter un arbre binaire, nous utiliserons une fonction non évaluée de la forme ARBRE(clef, valeur, fils_gauche, fils_droite) .
L'arbre vide, qui est un cas particulier d'arbre binaire, sera représenté par ARBRE( )
. Par exemple, l'arbre binaire
"f" 7 "c" 14
| |
|_ _____________|
|
"noeud" 21
sera représenté sous la forme:
arbre := ARBRE( "noeud",21, ARBRE( "f", 7, ARBRE( ), ARBRE( ) ), ARBRE( "c", 14, ARBRE( ), ARBRE( ) ) );
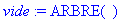
Création de types: Nous créons le type arbre_binaire permettant de représenter les arbres de Huffman:
|
> |
`type/arbre_binaire` := 'specfunc(anything,ARBRE)':
|
|
> |
arbre := ARBRE("noeud", 21, ARBRE("f",7,ARBRE(),ARBRE()), ARBRE("c", 14, ARBRE(), ARBRE()));
|
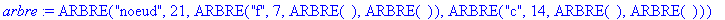
|
> |
type(arbre,'arbre_binaire' );
|
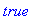
Fils_gauche, fils_droite: Les procédures fils_gauche (ou fils_droite
) retournent l'arbre binaire fils (ou enfant), éventuellement vide, de la branche gauche (ou droite) d'un arbre:
|
> |
fils_gauche := proc(arbre::arbre_binaire)
if arbre = vide then
error "Opération invalide (arbre vide)"
end if;
op(3,arbre)
end proc:
|

|
> |
fils_droite := proc(arbre::arbre_binaire)
if arbre = vide then
error "Opération invalide (arbre vide)"
end if;
op(4,arbre)
end proc:
|
|
> |
fils_droite(fils_gauche(arbre));
|

Représentation graphique:
|
>
|
with(plottools): with(plots):
|
Warning, the name arrow has been redefined
Les procédures feuille , noeud , et branche
permettent de représenter graphiquement les éléments constituant un arbre binaire:
|
> |
feuille:=proc(x,y,car,val)
polygon([[x,y], [x+3,y], [x+3,y+2],[x,y+2]], color=green, linestyle=1, thickness=1),
textplot([x+1.5,y+1.45,car],font=[HELVETICA,BOLD,14]),textplot([x+1.5,y+0.65,val])
end proc:
|
|
> |
noeud:=proc(x,y,car,val)
polygon([[x,y], [x+3,y], [x+3,y+2],[x,y+2]], color=gray, linestyle=1, thickness=1),
textplot([x+1.5,y+0.65,car],font=[HELVETICA,BOLD,14]),textplot([x+1.5,y+1.5,val])
end proc:
|
|
> |
branche:=proc(x,y,w,b)
local d;
d:=line([x,y], [x,y+1], color=black, linestyle=1),
line([x-w/2,y+1], [x+w/2,y+1], color=black, linestyle=1),
line([x-w/2,y+1], [x-w/2,y+2], color=black, linestyle=1),
line([x+w/2,y+1], [x+w/2,y+2], color=black, linestyle=1):
if b then d:=d,textplot([x-w/4,y+1.375,"1"], font=[HELVETICA,BOLD,10],color=red),
textplot([x+w/4,y+1.375,"0"],font=[HELVETICA,BOLD,10], color=red)
end if:
d
end proc: |
La procédure largeur permet de calculer récursivement la largeur d'un arbre binaire:
|
> |
largeur:=proc(arbre, F::list)
local s,calcul_largeur,T,k;
calcul_largeur := proc(arbre::arbre_binaire)
local d,g;
if arbre<>vide then
d:=fils_droite(arbre): g:=fils_gauche(arbre):
if d<>vide then
s:=s+3.5
end if;
if g<>vide then
s:=s+3.5
end if;
calcul_largeur(g): calcul_largeur(d)
end if
end proc:
if is(arbre,list) then 3.5
else
s:=0:
calcul_largeur(arbre);
if s=0 then s:=3 end if;
s;
end if
end proc:
|
|
> |
largeur(ARBRE("b",7,ARBRE(),ARBRE()),F);
|
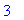
|
> |
largeur(ARBRE("noeud1",14,ARBRE("d",7,ARBRE(),ARBRE()),ARBRE("b",7,ARBRE(),ARBRE())),F);
|
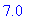
|
> |
largeur(ARBRE("noeud3",35,ARBRE("a",21,ARBRE(),ARBRE()),ARBRE("noeud1",14,ARBRE("d",7,ARBRE(),ARBRE()),
ARBRE("b",7,ARBRE(),ARBRE()))),F); |
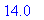
La procédure dessiner utilise les procédures précédentes pour représenter graphiquement un arbre binaire.
Elle sera utilisée dans la partie suivante, lors des différentes étapes de la constuction de l'arbre de Huffman.
|
> |
dessiner:=proc(L::list, b::truefalse)
local rep,k,t,w,w1,F;
global P,texte_source;
rep := proc(element,x,y,w)
local d,g;
if type(element,'arbre_binaire') then
if element<>vide then
d:=fils_droite(element): g:=fils_gauche(element):
if d=vide and g=vide then
P:=P,feuille(x,y,op(1,element),op(2,element))
else
P:=P,noeud(x,y,op(2,element),op(1,element)),branche(x+1.5,y+2,w,b):
end if:
if g<>vide then rep(g,x-w/2,y+4,largeur(g,F)*0.5) end if:
if d<>vide then rep(d,x+w/2,y+4,largeur(d,F)*0.5) end if:
end if:
else
P:=P,feuille(x,y,op(1,element),op(2,element))
end if
end proc:
P:=NULL: w:=0: F:=frequences(texte_source):
for k to nops(L) do
t:=largeur(L[k],F): w1:=w+0.5*(t-1): w:=w+t: rep(L[k],w1,0,t*0.5):
end do:
display(P,scaling=constrained,axes=none);
end proc:
|
Construction de l'arbre de Huffman:
Procédures auxiliaires: La procédure enlever retourne la liste L privée de son i-ème élément:
|
> |
enlever:=proc(i::posint,L::list)
local j,M;
M:=NULL;
for j to nops(L) do
if j<>i then M:=M,L[j] end if
end do;
[M];
end proc:
|
La procédure minis récupère les indices des éléments de L correspondant aux plus petites fréquences
(en parcourant la liste L de gauche à droite): |
> |
minis:=proc(L::list)
local M,i,j,m1,m2,v;
M:=L: v:=op(2,M[1]): m1:=1:
for j to nops(M) do
if op(2,M[j])<v then v:=op(2,M[j]): m1:=j end if
end do;
M:=enlever(m1,M);
v:=op(2,M[1]); m2:=1:
for j to nops(M) do
if op(2,M[j])<v then v:=op(2,M[j]): m2:=j end if
end do;
if m2>=m1 then m2:=m2+1 fi:
[m2,m1]
end proc:
|
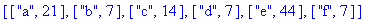 ![[4, 2]](images/huffman13.gif) Effectivement, en parcourant la liste F de gauche à droite, m1=2 correspondant au 2ème élément de la liste ("b" avec la fréquence
la plus faible: 7) et m2=4 correspondant au 4ème élément de la liste ("d" avec la seconde plus faible fréquence: 7) .
La procédure fusion permet de fusionner les 2 éléments de F correspondant aux éléments m[1] et m[2] de plus petite fréquence.
i désigne le n° de l'étape. Pour construire l'arbre binaire, il y aura nops(F)-1 étapes, donc nops(F)-1 appels à la
procédure fusion .
On remplace l'élément en position max(m[1],m[2]) dans F par l'élément obtenu par fusion (ajout des fréquences)
A la fin de la procédure, on retire un élément en position min(m[1],m[2]) dans F.
|
> |
fusion:=proc(F::list,i::posint)
local m,G;
G:=F: m:=minis(G);
if is(F[m[1]],list) then
if is(F[m[2]],list) then
G[max(m[1],m[2])]:=ARBRE(cat("noeud",i),op(2,F[m[1]])+op(2,F[m[2]]),ARBRE(op(1,F[m[1]]),op(2,F[m[1]]),
ARBRE(),ARBRE()),ARBRE(op(1,F[m[2]]),op(2,F[m[2]]),ARBRE(),ARBRE()))
else
G[max(m[1],m[2])]:=ARBRE(cat("noeud",i),op(2,F[m[1]])+op(2,F[m[2]]),
ARBRE(op(1,F[m[1]]),op(2,F[m[1]]),ARBRE(),ARBRE()),F[m[2]])
end if
else # F[m[1]] est un arbre
if is(F[m[2]],list) then
G[max(m[1],m[2])]:=ARBRE(cat("noeud",i),op(2,F[m[1]])+op(2,F[m[2]]),F[m[1]],
ARBRE(op(1,F[m[2]]),op(2,F[m[2]]),ARBRE(),ARBRE()))
else
G[max(m[1],m[2])]:=ARBRE(cat("noeud",i),op(2,F[m[1]])+op(2,F[m[2]]),F[m[1]],F[m[2]])
end if
end if:
enlever(min(m[1],m[2]),G)
end proc:
|
Pour comprendre le mécanisme de construction de l'arbre, détaillons étape par étape:
Les noeuds en gris (fusion) seront étiquetés "noeudk", où k est le n° de l'étape.
Etat initial :
Chaque feuille est étiquetée par le caractère auquel elle correspond, avec la fréquence correspondante, exemple: [ e , 44]. ![[Maple Bitmap]](images/huffman14.gif)
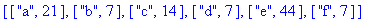
Etape 1 :
On fusionne d et b en un noeud étiqueté noeud1 avec pour fréquence la somme des fréquences des 2 caractères, soit 14. ![[Maple Bitmap]](images/huffman16.gif)
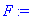
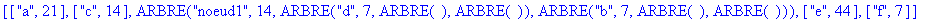
Etape 2 :
On fusionne c et f en un noeud étiqueté noeud2 avec pour fréquence la somme des fréquences des 2 caractères, soit 21. ![[Maple Bitmap]](images/huffman19.gif)
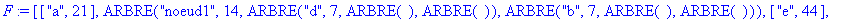
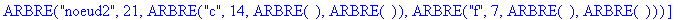
Etape 3 :
On fusionne a et noeud1 en un noeud étiqueté noeud3 avec pour fréquence la somme des fréquences des 2 nœuds, soit 35. ![[Maple Bitmap]](images/huffman22.gif)
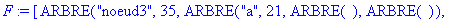
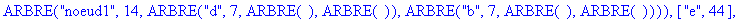
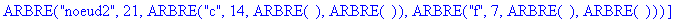
Etape 4 :
On fusionne noeud2 et noeud3 en un noeud étiqueté noeud4 avec pour fréquence la somme des fréquences des 2 nœuds, soit 56. ![[Maple Bitmap]](images/huffman26.gif)


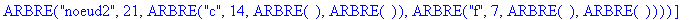
Etape 5 :
On fusionne e et noeud4 en un noeud étiqueté noeud5 avec pour fréquence la somme des fréquences des 2 nœuds, soit 100. ![[Maple Bitmap]](images/huffman30.gif)


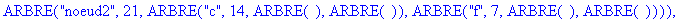

Procédure de construction: Pour construire l'arbre binaire de codage, on effectue nops(F)-1 appels successifs à la procédure fusion ,
ce qui est réalisé par la procédure construire_arbre : |
> |
construire_arbre:=proc(F::list)
local i,G;
G:=F: i:=0:
while nops(G)>1 do
i:=i+1: G:=fusion(G,i)
end do;
op(G)
end proc:
|
|
> |
F:=frequences(texte_source): A:=construire_arbre(F);
|


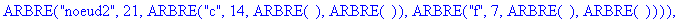

![[Maple Plot]](images/huffman39.gif)
Codage de Huffman:
Procédures de codage-décodage:
La procédure code(arbre,clef,c) attribue à un noeud (ou une feuille) de l'arbre binaire arbre défini(e) par sa clef
clef un code de Huffman c .
Ce code correspond à la façon dont on accède au noeud ou à la feuille dans l'arbre binaire:
code 1 pour une branche gauche, code 0 pour une branche droite.
Exemple 1 : dans l'arbre final (étape 5), pour accéder à la feuille correspondant au caractère d , on doit parcourir successivement les branches codées 1,1,0,1. Le code attribué à d sera donc 1101.
De même noeud1 sera codé 110.
|
> |
code := proc(arbre::arbre_binaire, clef::string, c::string)
local a;
if arbre<>vide then
if clef <> op(1,arbre) then
a:=code(fils_droite(arbre),clef,cat(c,"0")):
if a<>-1 then a else code(fils_gauche(arbre),clef,cat(c,"1")) end if
else
[c,clef]
end if
else
-1
end if
end proc:
|
|
> |
code(A,"d",""), code(A,"noeud1","");
|
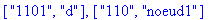
coder retourne une liste TD de décodage des feuilles de arbre . TD constituée d'éléments de la forme [ code , clef ]. |
> |
coder:=proc(arbre::arbre_binaire)
local k,L;
global F;
L:=NULL:
for k to nops(F) do L:=L,code(arbre,F[k][1],"") end do;
[L]
end proc:
|
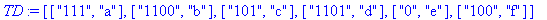
construire_listes construit à partir de la liste TD :
- la liste codes des codes de Huffman des caractères - la liste cars des caractères. |
> |
construire_listes:=proc()
local k;
global TD,codes,cars;
codes:=NULL: cars:=NULL:
for k to nops(TD) do
codes:=codes,TD[k][1]: cars:=cars,TD[k][2]
end do;
codes:=[codes]: cars:=[cars]
end proc:
|
|
> |
construire_listes(): codes; cars;
|
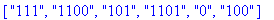 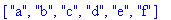
Taux de compression: Le taux de compression 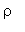 est défini par: est défini par: 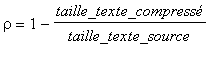 . . La procédure taux_compression calcule 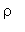 ( les tailles des textes source et compressé sont comptées en bits ). ( les tailles des textes source et compressé sont comptées en bits ).
Exemple 1 : un caractère du texte source comme e est codé sur 8 bits: 01100101. Ce même caractère codé selon Huffman ne nécessitera qu'un seul bit (le code étant 0)
|
> |
taux_compression:=proc(texte_source::string)
local k,rho,nbcaract,taille_texte_source,taille_texte_compresse,F,A,TD;
F:=frequences(texte_source):
A:=construire_arbre(F):
TD:=coder(A,F):
nbcaract:=convert([seq(F[k][2],k=1..nops(F))],`+`);
print(`Texte source: nombre de caractères `=nbcaract);
taille_texte_source:=8*nbcaract;
print(`Texte source: nombre de bits `=taille_texte_source);
taille_texte_compresse:=0;
for k to nops(TD) do
taille_texte_compresse:=taille_texte_compresse+length(TD[k][1])*F[k][2]:
end do;
print(`Texte compressé: nombre de bits `=taille_texte_compresse);
rho:=evalf(100*(1-taille_texte_compresse/taille_texte_source),4);
print(`Taux de compression en %`=rho)
end proc:
|
|
> |
taux_compression(texte_source);
|
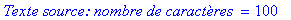 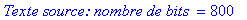  
Compression d'un fichier texte:
Lecture d'un fichier source:
La procédure lire_fichier lit un fichier texte défini par son nom:
(modifier au besoin le chemin du fichier)
|
> |
lire_fichier:=proc(nom::string)
local t,f,ligne,c;
t:="";
f:=FileTools[Text][Open](nom);
while not FileTools[AtEndOfFile](f) do
ligne := FileTools[Text][ReadLine](f);
t:=cat(t,ligne,"\n");
end do;
FileTools[Text][Close](f);
t;
end proc:
|
Exemple 2 On lit un texte de Rabelais à partir d'un fichier:
|
> |
texte_source:=lire_fichier("C:\\Maple\\Huffman\\Rabelais.txt");
|

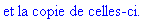



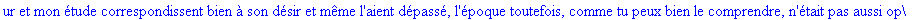


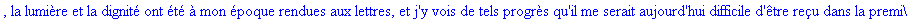


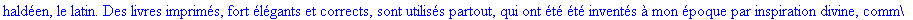





















|
> |
F:=frequences(texte_source);
|
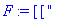
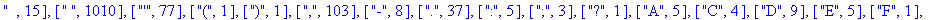
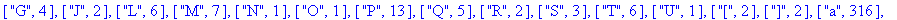
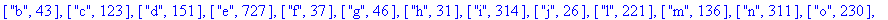
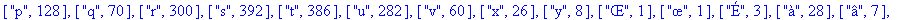
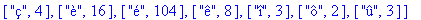
|
> |
A:=construire_arbre(F):
|
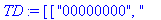
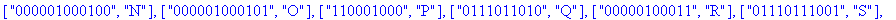
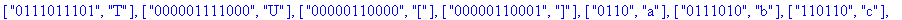
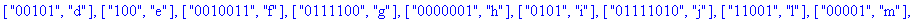
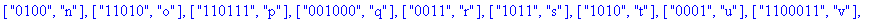
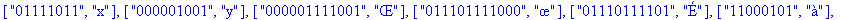
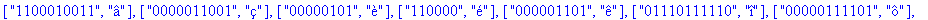
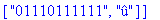
|
> |
taux_compression(texte_source);
|
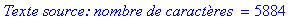 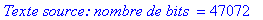 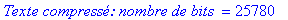  En fait, l'écriture de la table de décodage dans l'entête du fichier nous fera perdre un peu de ce pourcentage.
Ecriture de l'entête du fichier compressé: De façon à pouvoir récupérer ultérieurement lors de l'opération de décodage les caractères d'origine, on stocke dans une entête la table TD:
pour chaque élément de TD, de la forme [ code_huffman , caractère ] , on code code_huffman sur deux octets, sa longueur n sur un octet,
et le code hexadécimal de caractère sur un octet. C'est le travail effectué par la procédure entete : |
> |
entete:=proc(TD::list)
local c,d,j,k,n,s;
s:=nops(TD);
for k to nops(TD) do
d:=0: c:=TD[k][1]: n:=length(c):
for j from 0 to n-1 do d:=d+parse(c[n-j])*2^j od:
s:=s,iquo(d,256),irem(d,256),n,StringTools[Ord](TD[k][2])
end do:
[s]
end proc:
|
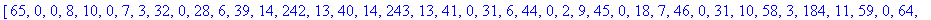
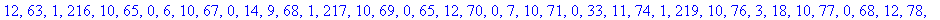
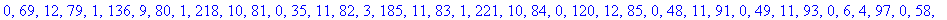
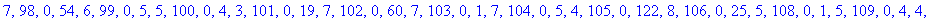
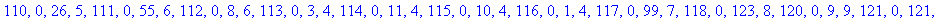
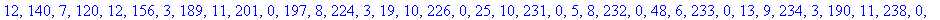
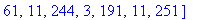 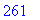 L'entête pour cet exemple a donc une taille de 261 octets.
Ecriture du texte compressé temporaire: La procédure texte_compresse_temporaire construit le texte compressé en remplaçant dans le texte source chaque caractère par son code de Huffman:
|
> |
texte_compresse_temporaire:=proc(texte::string)
local k,s,T;
global codes,cars;
s:="":
construire_listes():
for k to nops(cars) do
T[cars[k]]:=codes[k]
end do;
eval(T);
for k to length(texte) do
s:=cat(s,T[texte[k]])
od;
s
end proc:
|
|
> |
temp:=texte_compresse_temporaire(texte_source): |
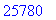 Le texte compressé pour cet exemple a donc une taille de 25780 bits (contre 47072 bits pour le texte source).
Ecriture du corps du fichier compressé: Comment stocker comme en mémoire une chaîne de caractères binaires 0,1 , ceux de
temp en l'occurrence?
C'est le travail effectué par la procédure corps .
On code d'abord la longueur de la chaîne sur 2 octets (on suppose longueur < 65536 = 16^4 = 64Ko) :
exemple: si la chaine a une longueur 60004, soit en hexa EA64
EA (hex) = 234 (dec) 64 (hex) = 100 (dec) donc on code la longueur 234 100
Si on fait des "paquets" de 8 caractères (octets) , on peut coder chaque "paquet" par un nombre entre 0 et 255.
Exemple:
"00001101" sera codé 2^3+2^2+2^0=13.
" 10000000 " sera codé 2^7= 128 .
Le pb est que la chaîne totale n'a pas toujours une longueur multiple de 8.
On regarde le reliquat, c'est à dire le reste modulo 8, on le code avec un nombre comme précédemment.
Exemple :
Un reliquat "0001" sera codé: 1
Ainsi "00001101 10000000 0001" sera codé 13 128 1 |
> |
corps:=proc(s::string)
local h,j,k,n,q,r,t,L;
n:=length(s);
L:=iquo(n,256),irem(n,256):
q:=iquo(n,8): r:=irem(n,8):
for j to q do
h:=0: for k from 0 to 7 do h:=h+parse(s[8-k+(j-1)*8])*2^k end do:
L:=L,h
end do:
if r>0 then
t:=substring(s,q*8+1..q*8+r):
h:=0: for k from 0 to r-1 do h:=h+parse(t[r-k])*2^k end do:
L:=L,h
end if:
[L]
end proc:
|
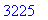 Le corps pour cet exemple a donc une taille de 3225 octets.
Ecriture sur disque du fichier compressé: La procédure ecrire_fichier_compresse écrit sur le disque le fichier défini par son nom:
(modifier au besoin le chemin du fichier)
|
> |
ecrire_fichier_compresse:=proc(nom::string)
local bytes,f,k,nb;
global TD,temp;
bytes:=[op(entete(TD)),op(corps(temp))]:
f:=open(nom,WRITE):
nb:=nops(bytes):
print(cat(nb,` octets`));
writebytes(f,[iquo(nb,256),irem(nb,256)]):
writebytes(f,bytes):
close(f)
end proc:
|
|
> |
ecrire_fichier_compresse("C:\\Maple\\Huffman\\Rabelais Comp.txt");
|
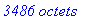 Pour cet exemple: au total 3486 octets ( 261 pour l'entête + 3225 pour le corps).
Lecture et décodage d'un fichier compressé:
Lecture d'un fichier compressé:
La procédure lire_fichier_compresse lit sur le disque le fichier compressé défini par son nom:
(modifier au besoin le chemin du fichier)
|
> |
lire_fichier_compresse:=proc(nom::string)
local f,nb,L,T;
f:=open(nom,READ);
L:=readbytes(f,2):
nb:=L[1]*256+L[2];
T:=readbytes(f,nb):
print(cat(nb,` octets`));
close(f):
T;
end proc:
|
|
> |
decode:=lire_fichier_compresse("C:\\Maple\\Huffman\\Rabelais Comp.txt"):
|
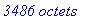 Pour cet exemple: lecture de 3486 octets.
Reconstitution de la table de décodage (entête du fichier): La procédure construire_entete reconstitue la table de décodage (entête du fichier compressé) à partir de la liste decod e.
|
> |
construire_entete:=proc(s::list)
local d,j,k,l,n,st,T;
T:=NULL;
n:=s[1]; # nb de caractères codés
for k to n do
d:=convert(s[4*k-2]*256+s[4*k-1],base,2):
st:="":
for j from 1 to nops(d) do st:=cat(convert(d[j],string),st) end do:
l:=length(st):
if s[4*k]>l then
for j to s[4*k]-l do st:=cat("0",st) end do
end if:
T:=T,[st,StringTools[Char](s[4*k+1])]
end do;
[T]
end proc:
|
|
> |
TD:=construire_entete(decode);
|
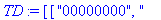
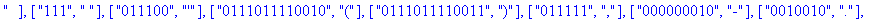
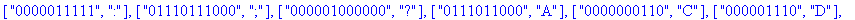
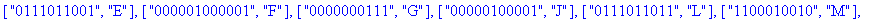
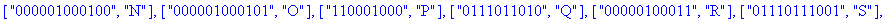
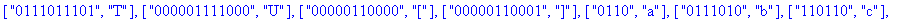
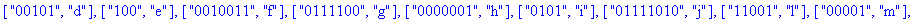
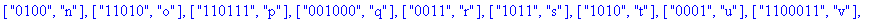
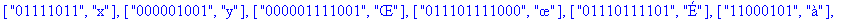
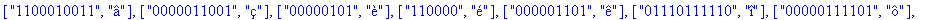
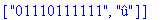
Reconstitution du corps du fichier: La procédure construire_corps reconstitue le corps du fichier compressé à partir de la liste decod e. |
> |
construire_corps:=proc(s::list)
local debut,n,q,r,i,j,k,t,L;
debut:=s[1]*4+2; # indice du début du corps
n:=s[debut]*256+s[debut+1]:
q:=iquo(n,8): r:=irem(n,8):
t:="":
for k from 1 to q do
if s[debut+k+1]=0 then L:=[0] else L:=convert(s[debut+k+1],base,2) end if:
j:=nops(L):
if j<8 then for i from 0 to 7-j do L:=[op(L),0] end do end if:
for i from nops(L) to 1 by -1 do t:=cat(t,L[i]) end do:
end do:
if r>0 then
if s[debut+q+2]=0 then L:=[0] else L:=convert(s[debut+q+2],base,2) end if:
j:=nops(L):
if j<r then for i from 0 to r-1-j do L:=[op(L),0] end do end if:
for i from nops(L) to 1 by -1 do t:=cat(t,L[i]) end do:
end if:
t
end proc:
|
|
> |
temp:=construire_corps(decode):
|
Décodage: La procédure auxiliaire membre retourne la place d'une chaîne de caractères s dans une liste de chaînes de caractères L:
|
> |
membre:=proc(s::string, L::list(string))
local k;
for k to nops(L) do
if s=L[k] then return k end if
end do:
return -1
end proc:
|
La procédure decoder effectue le décodage du corps du fichier et reconstitue ainsi le texte du fichier source:
|
> |
decoder:=proc(t::string)
local d,k,m,n,s,fin;
global codes,cars;
construire_listes();
n:=length(t): k:=1: d:="": s:=t[1]:
while k<n do
m:=membre(s,codes):
if m>0 then d:=cat(d,cars[m]): k:=k+1: s:=t[k]: else k:=k+1: s:=cat(s,t[k]) end if:
end do:
d
end proc:
|




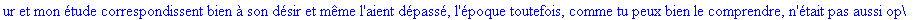


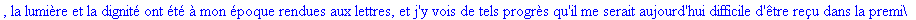






















©
- Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.
|

![[Maple OLE 2.0 Object]](images/huffman1.gif)
![[Maple Bitmap]](images/huffman3.gif)
![[Maple Bitmap]](images/huffman14.gif)
![[Maple Bitmap]](images/huffman16.gif)
![[Maple Bitmap]](images/huffman19.gif)
![[Maple Bitmap]](images/huffman22.gif)
![[Maple Bitmap]](images/huffman26.gif)
![[Maple Bitmap]](images/huffman30.gif)
![[Maple Plot]](images/huffman39.gif)
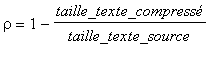 .
.