Apprendre Maple Caractérisation de quadriques

 
  Page d'accueilPage d'accueil   RechercherRechercher   Forum de discussionForum de discussion   ContactContact   SommaireSommaire 
  Cours MapleCours Maple   Travaux dirigésTravaux dirigés   Thèmes d'activitésThèmes d'activités   Thèmes d'activitésMaplets
Ecran MapleEcran Maple  TéléchargementTéléchargement  BibliographieBibliographie  LiensLiens  

 

 

Page d'accueil   Thèmes d'activités   << Thème précédent   Thème suivant >>

 

>   

restart:
with(linalg): with(plots):

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the name changecoords has been redefined

 

Soit un repère orthonormal (O, i , j, k) de E. Une quadrique est une surface notée S dont une équation dans ce repère s'écrit

f ( x, y,z ) = a[1]*`x²`+a[2]*`y²`+a[3]*`z²`+2*b[1]*y*z+2*b[2]*z*x+2*b[3]*x*y+2*c[1]*x+2*c[2]*y+2*c[3]*z+d  =0
 (avec a[1],a[2],a[3],b[1],b[2],b[3],c[1],c[2],c[3],dcoefficients réels)

On pose q( x, y, z  ) = a[1]*`x²`+a[2]*`y²`+a[3]*`z²`+2*b[1]*y*z+2*b[2]*z*x+2*b[3]*x*y

q est donc une forme quadratique (supposée non nulle) de E dont la matrice A  dans la base ( i, j, k ) s'écrit A = matrix([[a[1], b[3], b[2]], [b[3], a[2], b[1]], [b[2], b[1], a[3]]])

A est une matrice symétrique réelle, donc diagonalisable et il existe une base orthonormale B'=( e[1], e[2], e[3]  ) de E formée de vecteurs propres de A.

Diagonalisons la matrice dans une base orthonormale directe de vecteurs propres.On note  P la  matrice de passage de
( i,j,k ) vers B' et  lambda,mu,et nules trois valeurs propres de la matrice A.

Ainsi, la matrice A est semblable à matrix([[lambda, 0, 0], [0, mu, 0], [0, 0, nu]])  et q ( X*e[1]+Ye[2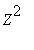] + Ze[3]   ) = lambda*X^2+mu*Y^2+nuZ^2.
B' est aussi une base q-orthogonale.


Premier cas : 0 n'est pas valeur propre de A

Dans ce cas, det(A) = lambda*mu*nu <> 0  . Alors S admet un centre de symétrie Omega(x[0],y[0],z[0])  dans (O, i , j, k ) où
(x[0], y[0], z[0]) vérifie le système :

Diff(f,x)*(x[0], y[0], z[0]) = 0  et Diff(f,y)*(x[0], y[0], z[0]) = 0  et Diff(f,z)*(x[0], y[0], z[0]) = 0

En effet, les formules X = x-x[0]  et Y = y-y[0]  et Z = z-z[0]  permettent d'obtenir l'équation de la quadrique dans ( Omega, i, j, k ):

a[1]*X^2+a[2]*Y^2+a[3]*Z^2+2*b[1]*Y*Z+2*b[2]*Z*X+2*b[3]*X*Y  = alpha  , les temes en x, y, et z disparaissant.

Ainsi S : q( Omega M) = alpha ,  s'écrit sous la forme S :   lambda*X^2+mu*Y^2+nuZ^2 =alpha  dans le repère (Omega,e[1], e[2],e[3]  ).

Sous cas 1

Si   alpha  = 0 , S : lambda*X^2+mu*Y^2  + nuZ^2= 0 est un cône du second degré de sommet Omega .

Si lambda, mu, nuont même signe alors X = Y = Z = 0 et donc S = {Omega}

Sinon, par exemple lambda,mu, ont même signe et S : X^2/(a^2)+Y^2/(b^2)-Z^2/(c^2) = 0est un cône elliptique.

Sous cas 2

Si alpha <> 0,X^2/alpha*lambda+Y^2/alpha*mu+Z^2/alpha*nu = 1


Si lambda, mu, nu  ont même signe, S est l'ensemble vide

                                   ou S : X^2/(a^2)+Y^2/(b^2)+Z^2/(c^2) = 1  est un ellipsoïde.

Sinon, par exemple lambda, mu, ont même signe et S : X^2/(a^2)+Y^2/(b^2)-Z^2/(c^2) = 1  est un hyperboloïde à une nappe

ou S : X^2/(a^2)+Y^2/(b^2)-Z^2/(c^2) = -1  est un hyperboloïde à deux nappes

Second cas : 0 est valeur propre simple de A

Dans ce cas, det(A) = 0. Si par exemple lambda <> 0 , mu <> 0  et nu = 0  on a alors :

q ( X*e[1]+Ye[2] + Ze[3]   ) = lambda*X^2+mu*Y^2  .

Dans ( O,e[1], e[2],e[3]),  l'équation de S s'écrit lambda*X^2+mu*Y^2+2*A[1]*X+2*B[1]*Y+2*C[1]*Z+D[1] = 0  que l'on peut mettre sous la forme

lambda*(X+A[1]/lambda)^2+mu*(Y+B[1]/mu)^2+2*C[1]*Z+D[1]' = 0

Sous cas 1

Si C[1]  = 0, soit Omega(-A[1]/lambda,-B[1]/mu,0)  dans ( O ,e[1], e[2],e[3]).

Dans ( O,e[1], e[2], e[3]), S : lambda*X^2+mu*Y^2 = alpha  est un cylindre de direction R e[3]  .

Sous cas i

Si alpha= 0 ,

Si lambda, muont même signe, alors X = Y = 0 . S est la droite ( Omega, e[3]).

Sinon, S est la réunion de 2 plans.

Sous cas ii

Si alpha <> 0

alors X^2/alpha*lambda+Y^2/alpha*mu = 1

Alors S est l'ensemble vide

    ou S : X^2/(a^2)+Y^2/(b^2) = 1  est un cylindre elliptique

    ou S : X^2/(a^2)-Y^2/(b^2) = 1  est un cylindre hyperbolique.

Sous cas 2

Si C[1] <> 0  dans  ( O,e[1], e[2],e[3]),    lambda*(X+A[1]/lambda)^2+mu*(Y+B[1]/mu)^2+2*C[1]*(Z+D[2]) = 0

Soit   Omega(-A[1]/lambda,-B[1]/mu,D[2]).Dans (Omega,e[1], e[2],e[3]), S : lambda*X^2+mu*Y^2+2*C[1]*Z = 0

Si lambda, mu  ont même signe, alors S : X^2/(a^2)+Y^2/(b^2) = Z/c  est un paraboloïde elliptique.

Sinon, X^2/(a^2)-Y^2/(b^2) = Z/c  est un paraboloïde hyperbolique.

Troisième cas : 0 est valeur propre double de A

Alors det(A)=0. Si par exemple lambda <> 0  et mu = nu= 0 on a alors q ( X*e[1]+Ye[2]+Ze[3]) = lambda*X^2

Dans ( O,e[1], e[2],e[3]),  l'équation de S s'écrit lambda*X^2+2*A[1]*X+2*B[1]*Y+2*C[1]*Z+D[1]= 0 que l'on peut mettre sous la forme  S : lambda*(X+A[1]/lambda)^2+2*B[1]*Y+2*C[1]*Z+D[1] = 0

Soit Omega(-A[1]/lambda,0,0) . Dans (Omega,e[1], e[2],e[3]), S : lambda*X^2+2*B[1]*Y+2*C[1]*Z+D[2] = 0

Si B[1] = C[1]  = 0 alors S : X^2 = k  . Donc S est l'ensemble vide

                                                    ou S est un plan

                                                    ou S est la réunion de 2 plans.

Si B[1] <> 0  ou C[1] <> 0 , soit e[3]' vecteur unitaire tel que { X=0 et B[1]*Y+C[1]*Z = 0 }, et e[2]'=e[3]' ^ e[1]    (produit vectoriel)

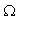L'équation de S dans (Omega,e[1], e[2]', e[3]') devient alors S : lambda*X^2+k*Y+D[2] = 0  avec k <> 0

Par changement d'origine, dans un repère  (Omega' ,e[1],e[2]' ,e[3]') , S a une équation de la forme S : X^2 = 2*p*Y

S est un cylindre parabolique de direction R e[3]'.


Cette feuille de calcul contient des procédures qui vont permettre de déterminer la nature de S et d'en donner les éléments caractéristiques ainsi que la représentation graphique.
  

Procédure Quadratique
Une expression expr est une forme quadratique en les variables X=[ x[1], x[2] ... x[n] ] si les 3 conditions sont vérifiées:

expr  vaut 0 au point [0,0,...,0].

Pour tout i , diff(expr,x[i])  vaut 0 au point [0,0,...,0], c'est à dire que la différentielle de expr  est nulle au point [0,0,...,0].

Pour tout ( i,j ),   diff(expr,x[j],x[i])  est une constante.
 

>    Quadratique:=proc(expr,X)
local d,d1,d2,i,j;
d:=subs(seq(X[i]=0,i=1..nops(X)),expr);
if d<>0 then return false fi;
for j to nops(X) do
  d1:=diff(expr,X[j]):
  d:=subs(seq(X[i]=0,i=1..nops(X)),d1);
  if d<>0 then return false fi;
od;
for i to nops(X) do
 for j to nops(X) do
   d2:=diff(expr,X[i],X[j]):
   if not type(d2,constant) then return false fi;
 od
od;
true
end proc:
 
>    q:=x^2+y^2+z^2-2*x*y+2*x*z: Quadratique(q,[x,y,z]);

true

Procédure ExtraireFormeQuad
Procédure d'extraction de la partie quadratique d'une expression expr  en X :
 

>    ExtraireFormeQuad:=proc(expr,X)
local e,q;
q:=0:
for e in expr do
  if Quadratique(e,X) then q:=q+e fi
end do:
q
end proc:
 
>    f:=x^2+y^2+z^2-2*x*y+2*x*z+3*x-y+z+1;

f := x^2+y^2+z^2-2*x*y+2*x*z+3*x-y+z+1

>    q:=ExtraireFormeQuad(f,[x,y,z]);

q := x^2+y^2+z^2-2*x*y+2*x*z

Procédure de calcul du centre de la quadrique
 

>    centre:=proc(expr,X)
local k,sys,c,s;
sys:={seq(diff(expr,X[i]),i=1..nops(X))};
s:=solve(sys,convert(X,set)):
c:=array(1..nops(X)):
for k to nops(s) do
  if lhs(s[k])=X[1] then c[1]:=rhs(s[k])
  elif lhs(s[k])=X[2] then c[2]:=rhs(s[k])
  else c[3]:=rhs(s[k]) fi
od:
convert(c,list)
end proc:
 
>    centre(f,[x,y,z]);

[1/2, 1, -1]

Procédure nouvelle_equation

Cette procédure effectue un changement de repère: connaissant l'équation f  dans l'ancien repère, la nouvelle origine pt ,
la matrice de passage P de l'ancienne à la nouvelle base, et les variables var , elle retourne l'équation  dans le nouveau repère.

>    nouvelle_equation:=proc(f,pt,P,var)
local k,X,Y,Z,x,y,nx,s;
nx:=[X,Y,Z]:
x:=matrix([seq([nx[i]],i=1..nops(var))]);
y:=evalm(P&*x);
s:=seq(var[k]=y[k,1]+pt[k],k=1..nops(var)); unapply(simplify(expand(subs(s,f))),op(1..nops(var),nx));
end proc:
 
>    collect(nouvelle_equation(f,[1/2, 1, -1],matrix([[0, 1/2*2^(1/2), -1/2*2^(1/2)], [1/2*2^(1/2), -1/2, -1/2], [1/2*2^(1/2), 1/2, 1/2]]),[x,y,z])(X,Y,Z),[X,Y,Z]);

X^2+(2^(1/2)+1)*Y^2+3/4+(-2^(1/2)+1)*Z^2

Procédure coord
coord  donne les valeurs numériques des coordonnées dans l'ancien repère (o,i,j,k) d'un point de coordonnées var  dans ( pt ,I,J,K). P  est la matrice de passage de l'ancienne à la nouvelle base.
Cette procédure servira pour tracer la quadrique dans le repère initial (o,i,j,k).
 

>    coord:=proc(var,pt,P)
local x,y;
x:=matrix([seq([var[i]],i=1..nops(var))]);
y:=evalm(P&*x);
seq(evalf(y[k,1]+pt[k]),k=1..nops(var))
end proc:
 
>    coord([1,2,3],[1/2, 1, -1],matrix([[0, 1/2*2^(1/2), -1/2*2^(1/2)], [1/2*2^(1/2), -1/2, -1/2], [1/2*2^(1/2), 1/2, 1/2]]));

-.2071067810, -.7928932190, 2.207106781

Procédure axes
Cette procédure trace les axes principaux de la quadrique:

>    axes:=proc(pt,P,tmin,tmax)
spacecurve([pt[1]+t*P[1,1],pt[2]+t*P[2,1],pt[3]+t*P[3,1],t=tmin..tmax],thickness=2,color=red),
spacecurve([pt[1]+t*P[1,2],pt[2]+t*P[2,2],pt[3]+t*P[3,2],t=tmin..tmax],thickness=2,color=red),
spacecurve([pt[1]+t*P[1,3],pt[2]+t*P[2,3],pt[3]+t*P[3,3],t=tmin..tmax],thickness=2,color=red)
end proc:
 

Procédure elements_car_cone_elliptique
Cette procédure donne les éléments caractéristiques d'un cône elliptique:

>    elements_car_cone_elliptique:=proc(eq,pt,P)
local a,b,c,param,surf:
print(`Quadrique à centre unique, surface réglée`);
a:=1/sqrt(abs(coeff(eq,X,2))): b:=1/sqrt(abs(coeff(eq,Y,2))): c:=1/sqrt(abs(coeff(eq,Z,2))):
if evalf(coeff(eq,X,2))<0 then
param:=[X=a*lambda,Y=b*lambda*cos(theta),Z=c*lambda*sin(theta)],theta=0..2*Pi,lambda=-infinity..infinity;
surf:=plot3d([coord([a*lambda,b*lambda*cos(theta),c*lambda*sin(theta)],pt,P)],theta=0..2*Pi,lambda=-100..100):
if b=c then print(`Cône de révolution d'axe (c,I)`) fi
elif evalf(coeff(eq,Y,2))<0 then
param:=[X=a*lambda*cos(theta),Y=b*lambda,Z=c*lambda*sin(theta)],theta=0..2*Pi,lambda=-infinity..infinity;
surf:=plot3d([coord([a*lambda*cos(theta),b*lambda,c*lambda*sin(theta)],pt,P)],theta=0..2*Pi,lambda=-100..100):
if a=c then print(`Cône de révolution d'axe (c,J)`) fi
else
param:=[X=a*lambda*cos(theta),Y=b*lambda*sin(theta),Z=c*lambda],theta=0..2*Pi,lambda=-infinity..infinity;
surf:=plot3d([coord([a*lambda*cos(theta),b*lambda*sin(theta),c*lambda],pt,P)],theta=0..2*Pi,lambda=-100..100):
if a=b then print(`Cône de révolution d'axe (c,K)`) fi
fi:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-100,100)},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure elements_car_ellipsoide
Cette procédure donne les éléments caractéristiques d'un ellipsoïde:

>    elements_car_ellipsoide:=proc(eq,pt,P)
local a,b,c,param,surf:
a:=1/sqrt(coeff(eq,X,2)): b:=1/sqrt(coeff(eq,Y,2)): c:=1/sqrt(coeff(eq,Z,2)):
print(`Quadrique à centre unique, surface non réglée`);
param:=[X=a*cos(phi)*cos(theta),Y=b*cos(phi)*sin(theta),Z=c*sin(phi)],theta=0..2*Pi,phi=-Pi/2..Pi/2;
surf:=plot3d([coord([a*cos(phi)*cos(theta),b*cos(phi)*sin(theta),c*sin(phi)],pt,P)],theta=0..2*Pi,phi=-Pi/2..Pi/2):
if a=b and b=c then print(`Sphère: rayon`=a)
else
if a=b then print(`Ellipsoïde de révolution d'axe (c,K)`) fi;
if b=c then print(`Ellipsoïde de révolution d'axe (c,I)`) fi;
if c=a then print(`Ellipsoïde de révolution d'axe (c,J)`) fi;
fi;
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-100,100)},labels=[x,y,z],axes=boxed,scaling=constrained,view=[pt[1]-a*1.5..pt[1]+a*1.5,pt[2]-b*1.5..pt[2]+b*1.5,pt[3]-c*1.5..pt[3]+c*1.5])
end proc:
 

Procédure elements_car_hyp1
Cette procédure donne les éléments caractéristiques d'un hyperboloïde à une nappe:

>    elements_car_hyp1:=proc(eq,pt,P)
local a,b,c,param,surf:
print(`Quadrique à centre unique, surface réglée`);
a:=1/sqrt(abs(coeff(eq,X,2))): b:=1/sqrt(abs(coeff(eq,Y,2))): c:=1/sqrt(abs(coeff(eq,Z,2))):
if evalf(coeff(eq,X,2))<0 then
param:=[X=a*sinh(phi),Y=b*cosh(phi)*cos(theta),Z=c*cosh(phi)*sin(theta)],theta=-infinity..infinity,phi=-infinity..infinity;
surf:=plot3d([coord([a*sinh(phi),b*cosh(phi)*cos(theta),c*cosh(phi)*sin(theta)],pt,P)],theta=0..2*Pi,phi=-arcsinh(10/a)..arcsinh(10/a)):
if b=c then print(`Hyperboloïde de révolution à une nappe d'axe (c,I)`) fi
elif evalf(coeff(eq,Y,2))<0 then
param:=[X=a*cosh(phi)*cos(theta),Y=b*sinh(phi),Z=c*cosh(phi)*sin(theta)],theta=-infinity..infinity,phi=-infinity..infinity;
surf:=plot3d([coord([a*cosh(phi)*cos(theta),b*sinh(phi),c*cosh(phi)*sin(theta)],pt,P)],theta=0..2*Pi,phi=-arcsinh(10/b)..arcsinh(10/b)):
if a=c then print(`Hyperboloïde de révolution à une nappe d'axe (c,J)`) fi
else
param:=[X=a*cosh(phi)*cos(theta),Y=b*cosh(phi)*sin(theta),Z=c*sinh(phi)],theta=-infinity..infinity,phi=-infinity..infinity;
surf:=plot3d([coord([a*cosh(phi)*cos(theta),b*cosh(phi)*sin(theta),c*sinh(phi)],pt,P)],theta=0..2*Pi,phi=-arcsinh(10/c)..arcsinh(10/c)):
if a=b then print(`Hyperboloïde de révolution à une nappe d'axe (c,K)`) fi
fi:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-10,10)},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure elements_car_hyp2
Cette procédure donne les éléments caractéristiques d'un hyperboloïde à deux nappes:

>    elements_car_hyp2:=proc(eq,pt,P)
local a,b,c,param,surf:
print(`Quadrique à centre unique, surface non réglée`);
a:=1/sqrt(abs(coeff(eq,X,2))): b:=1/sqrt(abs(coeff(eq,Y,2))): c:=1/sqrt(abs(coeff(eq,Z,2))):
if evalf(coeff(eq,X,2))<0 then
param:=[X=epsilon*a*cosh(phi),Y=b*sinh(phi)*cos(theta),Z=c*sinh(phi)*sin(theta)],theta=0..2*Pi,phi=-infinity..infinity,epsilon=±1;
surf:=plot3d([coord([a*cosh(phi),b*sinh(phi)*cos(theta),c*sinh(phi)*sin(theta)],pt,P)],theta=0..2*Pi,phi=-arccosh(10/a)..arccosh(10/a)),plot3d([coord([-a*cosh(phi),b*sinh(phi)*cos(theta),c*sinh(phi)*sin(theta)],pt,P)],theta=0..2*Pi,phi=-arccosh(10/a)..arccosh(10/a)):
if b=c then print(`Hyperboloïde de révolution à deux nappes d'axe (c,I)`) fi
elif evalf(coeff(eq,Y,2))<0 then
param:=[X=a*sinh(phi)*cos(theta),Y=epsilon*b*cosh(phi),Z=c*sinh(phi)*sin(theta)],theta=0..2*Pi,phi=-infinity..infinity,epsilon=±1;
surf:=plot3d([coord([a*sinh(phi)*cos(theta),b*cosh(phi),c*sinh(phi)*sin(theta)],pt,P)],theta=0..2*Pi,phi=-arccosh(10/b)..arccosh(10/b)),plot3d([coord([a*sinh(phi)*cos(theta),-b*cosh(phi),c*sinh(phi)*sin(theta)],pt,P)],theta=0..2*Pi,phi=-arccosh(10/b)..arccosh(10/b)):
if a=c then print(`Hyperboloïde de révolution à deux nappes d'axe (c,J)`) fi
else
param:=[X=a*sinh(phi)*cos(theta),Y=b*sinh(phi)*sin(theta),Z=epsilon*c*cosh(phi)],theta=-0..2*Pi,phi=-infinity..infinity,epsilon=±1;
surf:=plot3d([coord([a*sinh(phi)*cos(theta),b*sinh(phi)*sin(theta),c*cosh(phi)],pt,P)],theta=0..2*Pi,phi=-arccosh(10/c)..arccosh(10/c)),plot3d([coord([a*sinh(phi)*cos(theta),b*sinh(phi)*sin(theta),-c*cosh(phi)],pt,P)],theta=0..2*Pi,phi=-arccosh(10/c)..arccosh(10/c)):
if a=b then print(`Hyperboloïde de révolution à deux nappes d'axe (c,K)`) fi
fi:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-10,10)},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure elements_car_cyl_ell
Cette procédure donne les éléments caractéristiques d'un cylindre elliptique:

>    elements_car_cyl_ell:=proc(eq,pt,P)
local a,b,param,surf:
print(`Quadrique admettant une droite des centres (l'axe du cylindre), surface réglée`);
if evalf(coeff(eq,X,2))=0 then
a:=1/sqrt(abs(coeff(eq,Y,2))): b:=1/sqrt(abs(coeff(eq,Z,2))):
print(`Axe du cylindre: (s,I)`):
if a=b then print(`Cylindre de révolution d'axe (s,I), de rayon a`) fi:
param:=[X=lambda,Y=a*cos(theta),Z=b*sin(theta)],theta=0..2*Pi,lambda=-infinity..infinity:
surf:=plot3d([coord([lambda,a*cos(theta),b*sin(theta)],pt,P)],theta=0..2*Pi,lambda=-2..2):
elif evalf(coeff(eq,Y,2))=0 then
a:=1/sqrt(abs(coeff(eq,X,2))): b:=1/sqrt(abs(coeff(eq,Z,2))):
print(`Axe du cylindre: (s,J)`):
if a=b then print(`Cylindre de révolution d'axe (s,J), de rayon a`) fi:
param:=[X=a*cos(theta),Y=lambda, Z=b*sin(theta)],theta=0..2*Pi,lambda=-infinity..infinity:
surf:=plot3d([coord([a*cos(theta),lambda,b*sin(theta)],pt,P)],theta=0..2*Pi,lambda=-2..2):
else
a:=1/sqrt(abs(coeff(eq,X,2))): b:=1/sqrt(abs(coeff(eq,Y,2))):
print(`Axe du cylindre: (s,K)`):
if a=b then print(`Cylindre de révolution d'axe (s,K), de rayon a`) fi:
param:=[X=a*cos(theta),Y=b*sin(theta),Z=lambda],theta=0..2*Pi,lambda=-infinity..infinity:
surf:=plot3d([coord([a*cos(theta),b*sin(theta),lambda],pt,P)],theta=0..2*Pi,lambda=-2..2):
end if:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-max(a,b),max(a,b))},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure elements_car_cyl_hyp
Cette procédure donne les éléments caractéristiques d'un cylindre hyperbolique:

>    elements_car_cyl_hyp:=proc(eq,pt,P)
local a,b,c,param,surf:
print(`Quadrique admettant une droite des centres (l'axe du cylindre), surface réglée`);
if evalf(coeff(eq,X,2))=0 then
a:=1/sqrt(abs(coeff(eq,Y,2))): b:=1/sqrt(abs(coeff(eq,Z,2))):
print(`Axe du cylindre: (s,I)`):
param:=[X=lambda,Y=epsilon*a*cosh(theta),Z=b*sinh(theta)],theta=-infinity..infinity,lambda=-infinity..infinity,epsilon=±1:
surf:=plot3d([coord([lambda,a*cosh(theta),b*sinh(theta)],pt,P)],theta=-arcsinh(10/b)..arcsinh(10/b),lambda=-2..2),plot3d([coord([lambda,-a*cosh(theta),b*sinh(theta)],pt,P)],theta=-arcsinh(10/b)..arcsinh(10/b),lambda=-2..2):
elif evalf(coeff(eq,Y,2))=0 then
a:=1/sqrt(abs(coeff(eq,X,2))): b:=1/sqrt(abs(coeff(eq,Z,2))):
print(`Axe du cylindre: (s,J)`):
param:=[X=epsilon*a*cosh(theta),Y=lambda,Z=b*sinh(theta)],theta=-infinity..infinity,lambda=-infinity..infinity,epsilon=±1:
surf:=plot3d([coord([a*cosh(theta),lambda,b*sinh(theta)],pt,P)],theta=-arcsinh(10/b)..arcsinh(10/b),lambda=-2..2),plot3d([coord([-a*cosh(theta),lambda,b*sinh(theta)],pt,P)],theta=-arcsinh(10/b)..arcsinh(10/b),lambda=-2..2):
else
a:=1/sqrt(abs(coeff(eq,X,2))): b:=1/sqrt(abs(coeff(eq,Y,2))):
print(`Axe du cylindre: (s,K)`):
param:=[X=epsilon*a*cosh(theta),Y=b*sinh(theta),Z=lambda],theta=-infinity..infinity,lambda=-infinity..infinity,epsilon=±1:
surf:=plot3d([coord([a*cosh(theta),b*sinh(theta),lambda],pt,P)],theta=-arcsinh(10/b)..arcsinh(10/b),lambda=-2..2),plot3d([coord([-a*cosh(theta),b*sinh(theta),lambda],pt,P)],theta=-arcsinh(10/b)..arcsinh(10/b),lambda=-2..2):
end if:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-10,10)},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure elements_car_cyl_parab
Cette procédure donne les éléments caractéristiques d'un cylindre parabolique:

>    elements_car_cyl_parab:=proc(eq,pt,P)
local e,a,param,surf:
print(`Quadrique sans centre, surface réglée`);
if evalf(coeff(eq,X,2))<>0 then
  e:=isolate(eq,X^2):
  if diff(rhs(e),Y)<>0 then a:=diff(rhs(e),Y):
  param:=[X=lambda,Y=lambda^2/a,Z=mu],lambda=-infinity..infinity,mu=-infinity..infinity:
surf:=plot3d([coord([lambda,lambda^2/a,mu],pt,P)],lambda=-sqrt(abs(a)*10)..sqrt(abs(a)*10),mu=-5..5):
  else a:=diff(rhs(e),Z):
  param:=[X=lambda,Y=mu,Z=lambda^2/a],lambda=-infinity..infinity,mu=-infinity..infinity:
surf:=plot3d([coord([lambda,mu,lambda^2/a],pt,P)],lambda=-sqrt(abs(a)*10)..sqrt(abs(a)*10),mu=-5..5):
  fi:
elif evalf(coeff(eq,Y,2))<>0 then
  e:=isolate(eq,Y^2):
  if diff(rhs(e),X)<>0 then a:=diff(rhs(e),X):
  param:=[X=lambda^2/a,Y=lambda,Z=mu],lambda=-infinity..infinity,mu=-infinity..infinity:
surf:=plot3d([coord([lambda^2/a,lambda,mu],pt,P)],lambda=-sqrt(abs(a)*10)..sqrt(abs(a)*10),mu=-5..5):
  else a:=diff(rhs(e),Z):
  param:=[X=mu,Y=lambda,Z=lambda^2/a],lambda=-infinity..infinity,mu=-infinity..infinity:
surf:=plot3d([coord([mu,lambda,lambda^2/a],pt,P)],lambda=-sqrt(abs(a)*10)..sqrt(abs(a)*10),mu=-5..5):
  fi:
else
  e:=isolate(eq,Z^2):
  if diff(rhs(e),X)<>0 then a:=diff(rhs(e),X):
  param:=[X=lambda^2/a,Y=mu,Z=lambda],lambda=-infinity..infinity,mu=-infinity..infinity:
  surf:=plot3d([coord([lambda^2/a,mu,lambda],pt,P)],lambda=-5..5,mu=-5..5):
  else a:=diff(rhs(e),Y):
  param:=[X=mu,Y=lambda^2/a,Z=lambda],lambda=-infinity..infinity,mu=-infinity..infinity:
  surf:=plot3d([coord([mu,lambda^2/a,lambda],pt,P)],lambda=-5..5,mu=-5..5):
  fi:
fi:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-10,10)},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure elements_car_parab_ ell
Cette procédure donne les éléments caractéristiques d'un paraboloïde elliptique:

>    elements_parab_ell:=proc(eq,pt,P)
local a,b,c,param,surf:
print(`Quadrique sans centre, surface non réglée`);
if evalf(coeff(lhs(eq),X,2))=0 then
a:=1/sqrt(abs(coeff(lhs(eq),Y,2))): b:=1/sqrt(abs(coeff(lhs(eq),Z,2))): c:=1/coeff(rhs(eq),X,1):
param:=[X=c*lambda^2,Y=a*lambda*cos(theta),Z=b*lambda*sin(theta)],theta=0..2*Pi,lambda=-infinity..infinity:
surf:=plot3d([coord([c*lambda^2,a*lambda*cos(theta),b*lambda*sin(theta)],pt,P)],theta=0..2*Pi,lambda=-sqrt(10/abs(c))..sqrt(10/abs(c)));
if a=b then print(`Paraboloïde de révolution d'axe (s,I)`) fi
elif evalf(coeff(lhs(eq),Y,2))=0 then
a:=1/sqrt(abs(coeff(lhs(eq),X,2))): b:=1/sqrt(abs(coeff(lhs(eq),Z,2))): c:=1/coeff(rhs(eq),Y,1):
param:=[X=a*lambda*cos(theta),Y=c*lambda^2,Z=b*lambda*sin(theta)],theta=0..2*Pi,lambda=-infinity..infinity:
surf:=plot3d([coord([a*lambda*cos(theta),c*lambda^2,b*lambda*sin(theta)],pt,P)],theta=0..2*Pi,lambda=-sqrt(10/abs(c))..sqrt(10/abs(c)));
if a=b then print(`Paraboloïde de révolution d'axe (s,J)`) fi
else
a:=1/sqrt(abs(coeff(lhs(eq),X,2))): b:=1/sqrt(abs(coeff(lhs(eq),Y,2))): c:=1/coeff(rhs(eq),Z,1):
param:=[X=a*lambda*cos(theta),Y=b*lambda*sin(theta),Z=c*lambda^2],theta=0..2*Pi,lambda=-infinity..infinity:
surf:=plot3d([coord([a*lambda*cos(theta),b*lambda*sin(theta),c*lambda^2],pt,P)],theta=0..2*Pi,lambda=-sqrt(10/abs(c))..sqrt(10/abs(c)));
if a=b then print(`Paraboloïde de révolution d'axe (s,K)`) fi
fi:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-10,10)},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure elements_car_parab_ hyp
Cette procédure donne les éléments caractéristiques d'un paraboloïde hyperbolique:

>    elements_parab_hyp:=proc(eq,pt,P)
local a,b,c,param,surf:
print(`Quadrique sans centre, surface réglée`);
if evalf(coeff(lhs(eq),X,2))=0 then
a:=1/sqrt(abs(coeff(lhs(eq),Y,2))): b:=1/sqrt(abs(coeff(lhs(eq),Z,2))): c:=1/coeff(rhs(eq),X,1):
param:=[X=c*lambda^2,Y=a*lambda*cosh(theta),Z=b*lambda*sinh(theta)],theta=-infinity..infinity,lambda=-infinity..infinity:
surf:=plot3d([coord([c*lambda^2,a*lambda*cosh(theta),b*lambda*sinh(theta)],pt,P)],theta=-2.5..2.5,lambda=-sqrt(10/abs(c))..sqrt(10/abs(c)));
elif evalf(coeff(lhs(eq),Y,2))=0 then
a:=1/sqrt(abs(coeff(lhs(eq),X,2))): b:=1/sqrt(abs(coeff(lhs(eq),Z,2))): c:=1/coeff(rhs(eq),Y,1):
param:=[X=a*lambda*cosh(theta),Y=c*lambda^2,Z=b*lambda*sinh(theta)],theta=-infinity..infinity,lambda=-infinity..infinity:
surf:=plot3d([coord([a*lambda*cosh(theta),c*lambda^2,b*lambda*sinh(theta)],pt,P)],theta=-2.5..2.5,lambda=-sqrt(10/abs(c))..sqrt(10/abs(c)));
else
a:=1/sqrt(abs(coeff(lhs(eq),X,2))): b:=1/sqrt(abs(coeff(lhs(eq),Y,2))): c:=1/coeff(rhs(eq),Z,1):
param:=[X=a*lambda*cosh(theta),Y=b*lambda*sinh(theta),Z=c*lambda^2],theta=-infinity..infinity,lambda=-infinity..infinity:
surf:=plot3d([coord([a*lambda*cosh(theta),b*lambda*sinh(theta),c*lambda^2],pt,P)],theta=-2.5..2.5,lambda=-sqrt(10/abs(c))..sqrt(10/abs(c)));
fi:
print(`Paramétrage: `,param):
display({surf,axes(pt,P,-10,10)},labels=[x,y,z],axes=boxed,scaling=constrained)
end proc:
 

Procédure zero_pas_vp
Traitement du cas où 0 n'est pas valeur propre de la matrice de la forme quadratique associée:

>    zero_pas_vp:=proc(eq,c,P)
local alpha,lambda,mu,nu,e;
alpha:=-subs(X=0,Y=0,Z=0,eq);
lambda:=coeff(eq,X,2): mu:=coeff(eq,Y,2): nu:=coeff(eq,Z,2):
if evalf(alpha)=0 then # cône du second degré
  if evalf(lambda*mu)>0 and evalf(mu*nu)>0 then print(`Quadrique dégénérée, réduite au point c.`)
  else
    print(`Cône elliptique (ou du second degré) de sommet c:`);
    if evalf(lambda*mu)>0 then
      if evalf(lambda)>0 then e:=lambda*X^2+mu*Y^2+nu*Z^2 else                         e:=-lambda*X^2-mu*Y^2-nu*Z^2 fi
    elif evalf(lambda*nu)>0 then
      if evalf(lambda)>0 then e:=lambda*X^2+mu*Y^2+nu*Z^2 else          e:=-lambda*X^2-mu*Y^2-nu*Z^2 fi
    else
      if evalf(mu)>0 then e:=lambda*X^2+mu*Y^2+nu*Z^2 else e:=-lambda*X^2-mu*Y^2-nu*Z^2
    fi:
    print(e=0); elements_car_cone_elliptique(e,c,P)
  fi
fi
else # alpha<>0
  if evalf(lambda*mu)>0 and evalf(mu*nu)>0 then
    if evalf(alpha/lambda)<0 then print(`Quadrique dégénérée: ensemble vide`)
    else print(`Ellipsoïde de centre c`):
      e:=X^2/(alpha/lambda)+Y^2/(alpha/mu)+Z^2/(alpha/nu): print(e=1):
      elements_car_ellipsoide(e,c,P)
    fi
  else
    if evalf(lambda*mu)>0 then
      if evalf(alpha/lambda)>0 then
        print(`Hyperboloïde à une nappe de centre c`):
        e:=X^2/(alpha/lambda)+Y^2/(alpha/mu)+Z^2/(alpha/nu): print(e=1):
        elements_car_hyp1(e,c,P)  
      else print(`Hyperboloïde à deux nappes de centre c`):
        e:=X^2/(-alpha/lambda)+Y^2/(-alpha/mu)-Z^2/(alpha/nu): print(e=-1):
        elements_car_hyp2(e,c,P)
      fi
    elif evalf(lambda*nu)>0 then
      if evalf(alpha/lambda)>0 then
        print(`Hyperboloïde à une nappe de centre c`):
        e:=X^2/(alpha/lambda)+Y^2/(alpha/mu)+Z^2/(alpha/nu): print(e=1):
        elements_car_hyp1(e,c,P)
      else print(`Hyperboloïde à deux nappes de centre c`):
        e:=X^2/(-alpha/lambda)-Y^2/(alpha/mu)-Z^2/(alpha/nu): print(e=-1):
        elements_car_hyp2(e,c,P)
      fi
    else
      if evalf(mu*nu)>0 then
        if evalf(alpha/mu)>0 then
          print(`Hyperboloïde à une nappe de centre c`):
          e:=X^2/(alpha/lambda)+Y^2/(alpha/mu)+Z^2/(alpha/nu): print(e=1):
          elements_car_hyp1(e,c,P)
        else print(`Hyperboloïde à deux nappes de centre c`):
          e:=X^2/(-alpha/lambda)+Y^2/(-alpha/mu)+Z^2/(-alpha/nu): print(e=-1):
          elements_car_hyp2(e,c,P)
        fi
      fi
    fi
  fi  
fi
end proc:
 

Procédure zero_vp_ simple
Traitement du cas où 0 est une valeur propre simple de la matrice de la forme quadratique associée:

>    zero_vp_simple:=proc(eq,P)
local c1,d1,e,e1,s,alpha,lambda,mu,nu;
alpha:=-subs(X=0,Y=0,Z=0,eq);
lambda:=coeff(eq,X,2): mu:=coeff(eq,Y,2): nu:=coeff(eq,Z,2):
if evalf(lambda)=0 then c1:=coeff(eq,X)
elif evalf(mu)=0 then c1:=coeff(eq,Y)
else c1:=coeff(eq,Z) fi:

if c1=0 then
  if evalf(lambda)=0 then s:=[0,solve(diff(eq,Y),Y),solve(diff(eq,Z),Z)]
  elif evalf(mu)=0 then s:=[solve(diff(eq,X),X),0,solve(diff(eq,Z),Z)]
  else s:=[solve(diff(eq,X),X),solve(diff(eq,Y),Y),0] fi:
  print(`nouvelle origine de coordonnées dans [o,I,J,K]:   s`=map(simplify,s));
  e:=nouvelle_equation(subs(X=x,Y=y,Z=z,eq),s,diag(1,1,1),[x,y,z]):
  print(`équation dans (s,I,J,K):`);
  print(e(X,Y,Z)=0);
  alpha:=-subs(X=0,Y=0,Z=0,e(X,Y,Z));
  if evalf(alpha)=0 then
   if evalf(nu)=0 then
     if evalf(lambda*mu)>0 then print(`Quadrique dégénérée: droite (c,K)`): print(`X=Y=0`)
     else print(`Quadrique dégénérée: réunion de 2 plans`):
          print(Y=-sqrt(-lambda/mu)*X,Y=sqrt(-lambda/mu)*X);
     fi
    elif evalf(mu)=0 then
     if evalf(lambda*nu)>0 then print(`Quadrique dégénérée: droite (c,J)`): print(`X=Z=0`)
     else print(`Quadrique dégénérée: réunion de 2 plans`):
          print(Z=-sqrt(-lambda/nu)*X,Z=sqrt(-lambda/nu)*X);
     fi  
    else # evalf(lambda)=0 then
     if evalf(mu*nu)>0 then print(`Quadrique dégénérée: droite (c,I)`): print(`Y=Z=0`)
     else print(`Quadrique dégénérée: réunion de 2 plans`):
          print(Z=-sqrt(-mu/nu)*Y,Z=sqrt(-mu/nu)*Y);
     fi
    fi

 else # alpha<>0
   if evalf(nu)=0 then
      if evalf(alpha/lambda)<0 and evalf(alpha/mu)<0 then print(`Quadrique dégénérée: ensemble vide`)
      elif evalf(alpha/lambda)>0 and evalf(alpha/mu)>0 then print(`Cylindre elliptique`):
           e:=X^2/(alpha/lambda)+Y^2/(alpha/mu): print(e=1):
           elements_car_cyl_ell(e,s,P):
      else print(`Cylindre hyperbolique`):
           if evalf(alpha/lambda)>0 then e:=X^2/(alpha/lambda)+Y^2/(alpha/mu) else
           e:=Y^2/(alpha/mu)+X^2/(alpha/lambda) fi:
           print(e=1): elements_car_cyl_hyp(e,s,P):
      fi
    elif evalf(mu)=0 then
      if evalf(alpha/lambda)<0 and evalf(alpha/nu)<0 then print(`Quadrique dégénérée: ensemble vide`)
      elif evalf(alpha/lambda)>0 and evalf(alpha/nu)>0 then print(`Cylindre elliptique`):
           e:=X^2/(alpha/lambda)+Z^2/(alpha/nu)=1: print(e=1):
           elements_car_cyl_ell(e,s,P):
      else print(`Cylindre hyperbolique`):
           if evalf(alpha/lambda)>0 then e:=X^2/(alpha/lambda)+Z^2/(alpha/nu) else
           e:=Z^2/(alpha/nu)+X^2/(alpha/lambda) fi:
           print(e=1): elements_car_cyl_hyp(e,s,P)
      fi
    else
      if evalf(alpha/mu)<0 and evalf(alpha/nu)<0 then print(`Quadrique dégénérée: ensemble vide`)
      elif evalf(alpha/mu)>0 and evalf(alpha/nu)>0 then print(`Cylindre elliptique`):
           e:=Y^2/(alpha/mu)+Z^2/(alpha/nu): print(e=1):
           elements_car_cyl_ell(e,s,P):
       else print(`Cylindre hyperbolique`):
           if evalf(alpha/mu)>0 then e:=Y^2/(alpha/mu)+Z^2/(alpha/nu) else
           e:=Z^2/(alpha/nu)+Y^2/(alpha/mu) fi: print(e=1):
           elements_car_cyl_hyp(e,s,P)
      fi
    fi   
  fi

else # c1 non nul
  if evalf(lambda)=0 then s:=[0,solve(diff(eq,Y),Y),solve(diff(eq,Z),Z)]
  elif evalf(mu)=0 then s:=[solve(diff(eq,X),X),0,solve(diff(eq,Z),Z)]
  else s:=[solve(diff(eq,X),X),solve(diff(eq,Y),Y),0] fi:
  e1:=nouvelle_equation(subs(X=x,Y=y,Z=z,eq),s,diag(1,1,1),[x,y,z]):
  if evalf(lambda)=0 then s[1]:=solve(subs(Y=0,Z=0,e1(X,Y,Z)),X)
  elif evalf(mu)=0 then s[2]:=solve(subs(X=0,Z=0,e1(X,Y,Z)),Y)
  else s[3]:=solve(subs(X=0,Y=0,e1(X,Y,Z)),Z) fi:
  print(`nouvelle origine de coordonnées dans [o,I,J,K]:   s`=map(simplify,s));
  e:=nouvelle_equation(subs(X=x,Y=y,Z=z,eq),s,diag(1,1,1),[x,y,z]):
  print(`équation dans (s,I,J,K):`);
  print(e(X,Y,Z)=0);

  e1:=["",0]:
  if evalf(nu)=0 then
    if evalf(lambda*mu)>0 then
      print(`Paraboloïde elliptique`); e1[1]:="ell":
    else print(`Paraboloïde hyperbolique`): e1[1]:="hyp" fi;
    if evalf(lambda)>0 then e1[2]:=lambda*X^2+mu*Y^2=-coeff(e(X,Y,Z),Z)*Z else
    e1[2]:=-lambda*X^2-mu*Y^2=coeff(e(X,Y,Z),Z)*Z fi:
  elif evalf(mu)=0 then
    if evalf(lambda*nu)>0 then
      print(`Paraboloïde elliptique`); e1[1]:="ell":
    else print(`Paraboloïde hyperbolique`): e1[1]:="hyp" fi;
    if evalf(lambda)>0 then e1[2]:=lambda*X^2+nu*Z^2=-coeff(e(X,Y,Z),Y)*Y else
    e1[2]:=-lambda*X^2-nu*Z^2=coeff(e(X,Y,Z),Y)*Y fi
  else
    if evalf(mu*nu)>0 then
      print(`Paraboloïde elliptique`); e1[1]:="ell":
    else print(`Paraboloïde hyperbolique`): e1[1]:="hyp" fi;
    if evalf(mu)>0 then e1[2]:=mu*Y^2+nu*Z^2=-coeff(e(X,Y,Z),X)*X else
    e1[2]:=-mu*Y^2-nu*Z^2=coeff(e(X,Y,Z),X)*X fi  
  fi:
  print(e1[2]);
  if e1[1]="ell" then elements_parab_ell(e1[2],s,P) else
  elements_parab_hyp(e1[2],s,P) fi;
fi
end proc:
 

Procédure zero_vp_double
Traitement du cas où 0 est une valeur propre double de la matrice de la forme quadratique associée:

>    zero_vp_double:=proc(eq,P)
local e,s,b1,c1,e1,t,alpha,beta,gamma,lambda,mu,nu,sys,sol,X1,Y1,Z1,U,V,W;
lambda:=coeff(eq,X,2): mu:=coeff(eq,Y,2): nu:=coeff(eq,Z,2):
if lambda<>0 then s:=[solve(diff(eq,X),X),0,0]
elif mu<>0 then s:=[0,solve(diff(eq,Y),Y),0]
else s:=[0,0,solve(diff(eq,Z),Z)] fi:
print(`nouvelle origine de coordonnées dans [o,I,J,K]:   s`=map(simplify,s));
e:=nouvelle_equation(subs(X=x,Y=y,Z=z,eq),s,diag(1,1,1),[x,y,z]):
print(`équation dans (s,I,J,K):`);
print(e(X,Y,Z)=0);

if evalm(lambda)<>0 then b1:=coeff(e(X,Y,Z),Y): c1:=coeff(e(X,Y,Z),Z)
elif evalm(mu)<>0 then b1:=coeff(e(X,Y,Z),X): c1:=coeff(e(X,Y,Z),Z)
else b1:=coeff(e(X,Y,Z),X):c1:=coeff(e(X,Y,Z),Y) fi:

if b1=0 and c1=0 then
  if evalm(lambda)<>0 then e1:=isolate(e(X,Y,Z),X^2)
  elif evalm(mu)<>0 then e1:=isolate(e(X,Y,Z),Y^2)
  else e1:=isolate(e(X,Y,Z),Z^2)
  fi:
  print(e1);
  if evalf(rhs(e1))<0 then print(`Quadrique dégénérée: ensemble vide`)
  elif evalf(rhs(e1))=0 then print(`Quadrique dégénérée. Plan d'équation:`):
    if evalm(lambda)<>0 then print(X=0)
    elif evalm(mu)<>0 then print(Y=0) else print(Z=0) fi:
  else print(`Quadrique dégénérée. Réunion de 2 plans d'équation:`):
    if evalm(lambda)<>0 then print(X=-sqrt(rhs(e1)),X=sqrt(rhs(e1)))
    elif evalm(mu)<>0 then print(Y=-sqrt(rhs(e1)),Y=sqrt(rhs(e1))) else         print(Z=-sqrt(rhs(e1)),Z=sqrt(rhs(e1))) fi:
  fi

else #b1<>0 ou c1<>0
  if evalm(lambda)<>0 then
    sys:={X1=0,b1*Y1+c1*Z1=0,X1^2+Y1^2+Z1^2=1}:
    U:=vector([1,0,0]):
    sol:=solve(sys,{X1,Y1,Z1}); assign(sol):
    W:=vector([X1,Y1,Z1]); V:=crossprod(W,U):
  elif evalm(mu)<>0 then
    sys:={Y1=0,b1*X1+c1*Z1=0,X1^2+Y1^2+Z1^2=1}:
    V:=vector([0,1,0]):
    sol:=solve(sys,{X1,Y1,Z1}); assign(sol):
    U:=vector([X1,Y1,Z1]); W:=crossprod(U,V):
  else
    sys:={Z1=0,b1*Y1+c1*Z1=0,X1^2+Y1^2+Z1^2=1}:
    W:=vector([0,0,1]):
    sol:=solve(sys,{X1,Y1,Z1}); assign(sol):
    V:=vector([X1,Y1,Z1]); U:=crossprod(V,W):
  fi:
  print(`changement de base (coordonnées dans (I,J,K))`):
  print(` U`=evalm(U),` V`=evalm(V),` W`=evalm(W));   
  e1:=nouvelle_equation(e(x,y,z),[0,0,0],concat(U,V,W),[x,y,z]);
  print(`équation dans (s,U,V,W):`);
  print(e1(X,Y,Z)=0);
  if evalm(lambda)<>0 then
    alpha:=coeff(e1(X,Y,Z),Y,1): beta:=subs(X=0,Y=0,Z=0,e1(X,Y,Z)):
    gamma:=-beta/alpha; t:=[0,gamma,0];
  elif evalm(mu)<>0 then
    alpha:=coeff(e1(X,Y,Z),Z,1): beta:=subs(X=0,Y=0,Z=0,e1(X,Y,Z)):
    gamma:=-beta/alpha; t:=[0,0,gamma];
  else
    alpha:=coeff(e1(X,Y,Z),X,1): beta:=subs(X=0,Y=0,Z=0,e1(X,Y,Z)):
    gamma:=-beta/alpha; t:=[gamma,0,0];
  fi:
  print(`nouvelle origine de coordonnées dans [s,U,V,W]:  t`=t):
  print(`Cylindre parabolique`);
  print(`équation dans (t,U,V,W):`);   
  e:=nouvelle_equation(e1(x,y,z),t,diag(1,1,1),[x,y,z]):
  print(e(X,Y,Z)=0);
  elements_car_cyl_parab(e(X,Y,Z),t,P):  
fi  
end proc:
 

Procédure quadrique
C'est la procédure principale de cette feuille de calcul. Elle reçoit en paramètres une expression expr des variables var .
Elle extrait la forme quadratique q  associée à expr , réduit sa matrice, calcule une base [I,J,K] de R^3orthonormale et qui est aussi q -orthogonale, analyse la nature de la quadrique et donne ses éléments caractéristiques, ainsi que sa représentation graphique

>    quadrique:=proc(expr,var)
local e,k,q,v,A,D,G,P,c,eq,vp,ker,s;
q:=ExtraireFormeQuad(expr,var);
for k in expr-q do
  if not type(k,constant) then
    for v in var do
      if not type(diff(k,v),constant) then error "Cette expression ne correspond pas à la forme attendue: Ax²+By²+Cz²+2Dxy+2Eyz+2Fzx+Gx+Hy+Iz+J" fi
    od
  fi
od;
if q=0 then error "Forme quadratique associée nulle" fi:
print(`Forme quadratique associée:  q`=q);
print(`Matrice de la forme quadratique associée:`);
A:=matrix([seq([seq(diff(q,var[i],var[j])/2,j=1..3)],i=1..3)]);
print(`A `=evalm(A));
vp:=sort([eigenvals(A)]):
print(`Valeur propres de A `=vp);
D:=jordan(A,'P1');
print(`Matrice diagonale semblable à A:   D`=evalm(D));
G:=map(normalize, GramSchmidt([col(P1,1..3)]));
P:=map(simplify,concat(op(G)));
print(`Matrice de passage orthogonale:   P`=evalm(P));
print(`Directions principales de la quadrique:`);
print(`I `=col(P,1),` J `=col(P,2), ` K `=col(P,3));
if det(D)<>0 then
  c:=centre(expr,var): print(`Quadrique à centre:   c`=c):
  print(`Equation dans (c,I,J,K): `):
  eq:=nouvelle_equation(f,c,P,var):
  print(collect(eq(X,Y,Z),[X,Y,Z])=0):
  zero_pas_vp(eq(X,Y,Z),c,P)
else # det(D)=0
  print(`Equation dans (o,I,J,K): `):
  eq:=nouvelle_equation(f,[0,0,0],P,var):
  print(eq(X,Y,Z)=0);
  ker:=nullspace(D);
  if nops(ker)=1 then # 0 valeur propre simple
    zero_vp_simple(eq(X,Y,Z),P)
  else
    if nops(ker)=2 then # 0 valeur propre double
       zero_vp_double(eq(X,Y,Z),P)
    fi
  fi
fi
end:
 

Exemple 1: Affichage d'un message d'erreur  

>    f:=x^4+y^4+z^4-2*x*y+2*x*z+3*x-y+z+1; quadrique(f,[x,y,z]);

f := x^4+y^4+z^4-2*x*y+2*x*z+3*x-y+z+1 

Error, (in quadrique) Cette expression ne correspond pas à la forme attendue: Ax²+By²+Cz²+2Dxy+2Eyz+2Fzx+Gx+Hy+Iz+J

Exemple 2: Un cas de dégénérescence

>    f:=-2*x^2+4*x*y-4*x*z-2*y^2+4*y*z-2*z^2+4*x-4*y+4*z+7; quadrique(f,[x,y,z]);

f := -2*x^2+4*x*y-4*x*z-2*y^2+4*y*z-2*z^2+4*x-4*y+4*z+7

`Forme quadratique associée:  q` = -2*z^2+4*y*z-2*y^2-4*x*z+4*x*y-2*x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[-2, 2, -2], [2, -2, 2], [-2, 2, -2]])

`Valeur propres de A ` = [-6, 0, 0]

`Matrice diagonale semblable à A:   D` = matrix([[0, 0, 0], [0, -6, 0], [0, 0, 0]])

`Matrice de passage orthogonale:   P` = matrix([[-1/6*2^(1/2)*3^(1/2), 1/3*3^(1/2), -1/2*2^(1/2)], [1/6*2^(1/2)*3^(1/2), -1/3*3^(1/2), -1/2*2^(1/2)], [1/3*2^(1/2)*3^(1/2), 1/3*3^(1/2), 0]])

`Directions principales de la quadrique:`

`I ` = vector([-1/6*2^(1/2)*3^(1/2), 1/6*2^(1/2)*3^(1/2), 1/3*2^(1/2)*3^(1/2)]), ` J ` = vector([1/3*3^(1/2), -1/3*3^(1/2), 1/3*3^(1/2)]), ` K ` = vector([-1/2*2^(1/2), -1/2*2^(1/2), 0])

`Equation dans (o,I,J,K): `

7+4*3^(1/2)*Y-6*Y^2 = 0

`nouvelle origine de coordonnées dans [o,I,J,K]:   s` = [0, 1/3*3^(1/2), 0]

`équation dans (s,I,J,K):`

9-6*Y^2 = 0

Y^2 = 3/2

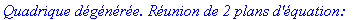
`Quadrique dégénérée. Réunion de 2 plans d'équation:`

Y = -1/2*6^(1/2), Y = 1/2*6^(1/2)

Exemple 3: Hyperboloïde à deux nappes

>    f:=x^2+y^2+z^2-2*x*y+2*x*z+3*x-y+z+1; quadrique(f,[x,y,z]);

f := x^2+y^2+z^2-2*x*y+2*x*z+3*x-y+z+1

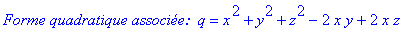
`Forme quadratique associée:  q` = x^2+y^2+z^2-2*x*y+2*x*z

`Matrice de la forme quadratique associée:`

`A ` = matrix([[1, -1, 1], [-1, 1, 0], [1, 0, 1]])

`Valeur propres de A ` = [1, 1-2^(1/2), 2^(1/2)+1]

`Matrice diagonale semblable à A:   D` = matrix([[1, 0, 0], [0, 1-2^(1/2), 0], [0, 0, 2^(1/2)+1]])

`Matrice de passage orthogonale:   P` = matrix([[0, -1/2*2^(1/2), 1/2*2^(1/2)], [1/2*2^(1/2), -1/2, -1/2], [1/2*2^(1/2), 1/2, 1/2]])

`Directions principales de la quadrique:`

`I ` = vector([0, 1/2*2^(1/2), 1/2*2^(1/2)]), ` J ` = vector([-1/2*2^(1/2), -1/2, 1/2]), ` K ` = vector([1/2*2^(1/2), -1/2, 1/2])

`Quadrique à centre:   c` = [1/2, 1, -1]

`Equation dans (c,I,J,K): `

X^2+(1-2^(1/2))*Y^2+3/4+(2^(1/2)+1)*Z^2 = 0

`Hyperboloïde à deux nappes de centre c`

4/3*X^2+4/3*(1-2^(1/2))*Y^2+4/3*(2^(1/2)+1)*Z^2 = -1

`Quadrique à centre unique, surface non réglée`

`Paramétrage: `, [X = 1/2*3^(1/2)*sinh(phi)*cos(theta), Y = 3/2*epsilon/(-3+3*2^(1/2))^(1/2)*cosh(phi), Z = 3/2*1/(3+3*2^(1/2))^(1/2)*sinh(phi)*sin(theta)], theta = 0 .. 2*Pi, phi = -infinity .. infini...

[Maple Plot]

Exemple 4: Cylindre elliptique

>    f:=x^2+2*y^2+z^2-2*y*z+2*x*y-2*x+2*y-4*z+4; quadrique(f,[x,y,z]);

f := x^2+2*y^2+z^2-2*y*z+2*x*y-2*x+2*y-4*z+4

`Forme quadratique associée:  q` = 2*x*y-2*y*z+z^2+2*y^2+x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[1, 1, 0], [1, 2, -1], [0, -1, 1]])

`Valeur propres de A ` = [0, 1, 3]

`Matrice diagonale semblable à A:   D` = matrix([[0, 0, 0], [0, 1, 0], [0, 0, 3]])

`Matrice de passage orthogonale:   P` = matrix([[1/3*3^(1/2), 1/2*2^(1/2), 1/6*6^(1/2)], [-1/3*3^(1/2), 0, 1/3*6^(1/2)], [-1/3*3^(1/2), 1/2*2^(1/2), -1/6*6^(1/2)]])

`Directions principales de la quadrique:`

`I ` = vector([1/3*3^(1/2), -1/3*3^(1/2), -1/3*3^(1/2)]), ` J ` = vector([1/2*2^(1/2), 0, 1/2*2^(1/2)]), ` K ` = vector([1/6*6^(1/2), 1/3*6^(1/2), -1/6*6^(1/2)])

`Equation dans (o,I,J,K): `

4-3*2^(1/2)*Y+2^(1/2)*3^(1/2)*Z+Y^2+3*Z^2 = 0

`nouvelle origine de coordonnées dans [o,I,J,K]:   s` = [0, 3/2*2^(1/2), -1/6*2^(1/2)*3^(1/2)]

`équation dans (s,I,J,K):`

-1+Y^2+3*Z^2 = 0

`Cylindre elliptique`

Y^2+3*Z^2 = 1

`Quadrique admettant une droite des centres (l'axe du cylindre), surface réglée`

`Axe du cylindre: (s,I)`

`Paramétrage: `, [X = lambda, Y = cos(theta), Z = 1/3*3^(1/2)*sin(theta)], theta = 0 .. 2*Pi, lambda = -infinity .. infinity

[Maple Plot]

Exemple 5: Hyperboloïde à une nappe

>    f:=x*y+y*z+x*z+2*y+1; quadrique(f,[x,y,z]);

f := x*y+y*z+x*z+2*y+1

`Forme quadratique associée:  q` = x*z+y*z+x*y

`Matrice de la forme quadratique associée:`

`A ` = matrix([[0, 1/2, 1/2], [1/2, 0, 1/2], [1/2, 1/2, 0]])

`Valeur propres de A ` = [-1/2, -1/2, 1]

`Matrice diagonale semblable à A:   D` = matrix([[1, 0, 0], [0, -1/2, 0], [0, 0, -1/2]])

`Matrice de passage orthogonale:   P` = matrix([[1/3*3^(1/2), -1/6*2^(1/2)*3^(1/2), -1/2*2^(1/2)], [1/3*3^(1/2), -1/6*2^(1/2)*3^(1/2), 1/2*2^(1/2)], [1/3*3^(1/2), 1/3*2^(1/2)*3^(1/2), 0]])

`Directions principales de la quadrique:`

`I ` = vector([1/3*3^(1/2), 1/3*3^(1/2), 1/3*3^(1/2)]), ` J ` = vector([-1/6*2^(1/2)*3^(1/2), -1/6*2^(1/2)*3^(1/2), 1/3*2^(1/2)*3^(1/2)]), ` K ` = vector([-1/2*2^(1/2), 1/2*2^(1/2), 0])

`Quadrique à centre:   c` = [-1, 1, -1]

`Equation dans (c,I,J,K): `

2+X^2-1/2*Y^2-1/2*Z^2 = 0

`Hyperboloïde à une nappe de centre c`

-1/2*X^2+1/4*Y^2+1/4*Z^2 = 1

`Quadrique à centre unique, surface réglée`

`Hyperboloïde de révolution à une nappe d'axe (c,I)`

`Paramétrage: `, [X = 2^(1/2)*sinh(phi), Y = 2*cosh(phi)*cos(theta), Z = 2*cosh(phi)*sin(theta)], theta = -infinity .. infinity, phi = -infinity .. infinity

[Maple Plot]

Exemple 6: Cône elliptique

>    f:=x^2-10*x-20-y^2+14*y+9*z^2-12*z; quadrique(f,[x,y,z]);

f := x^2-10*x-20-y^2+14*y+9*z^2-12*z

`Forme quadratique associée:  q` = 9*z^2-y^2+x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[1, 0, 0], [0, -1, 0], [0, 0, 9]])

`Valeur propres de A ` = [-1, 1, 9]

`Matrice diagonale semblable à A:   D` = matrix([[-1, 0, 0], [0, 1, 0], [0, 0, 9]])

`Matrice de passage orthogonale:   P` = matrix([[0, 1, 0], [1, 0, 0], [0, 0, 1]])

`Directions principales de la quadrique:`

`I ` = vector([0, 1, 0]), ` J ` = vector([1, 0, 0]), ` K ` = vector([0, 0, 1])

`Quadrique à centre:   c` = [5, 7, 2/3]

`Equation dans (c,I,J,K): `

Y^2-X^2+9*Z^2 = 0

`Cône elliptique (ou du second degré) de sommet c:`

Y^2-X^2+9*Z^2 = 0

`Quadrique à centre unique, surface réglée`

`Paramétrage: `, [X = lambda, Y = lambda*cos(theta), Z = 1/3*lambda*sin(theta)], theta = 0 .. 2*Pi, lambda = -infinity .. infinity

[Maple Plot]

Exemple 7: Ellipsoïde

>    f:=-2*x^2-4*x-75-4*y^2-10*y-3*z^2+30*z; quadrique(f,[x,y,z]);

f := -2*x^2-4*x-75-4*y^2-10*y-3*z^2+30*z

`Forme quadratique associée:  q` = -3*z^2-4*y^2-2*x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[-2, 0, 0], [0, -4, 0], [0, 0, -3]])

`Valeur propres de A ` = [-4, -3, -2]

`Matrice diagonale semblable à A:   D` = matrix([[-4, 0, 0], [0, -3, 0], [0, 0, -2]])

`Matrice de passage orthogonale:   P` = matrix([[0, 0, 1], [1, 0, 0], [0, 1, 0]])

`Directions principales de la quadrique:`

`I ` = vector([0, 1, 0]), ` J ` = vector([0, 0, 1]), ` K ` = vector([1, 0, 0])

`Quadrique à centre:   c` = [-1, -5/4, 5]

`Equation dans (c,I,J,K): `

-2*Z^2+33/4-4*X^2-3*Y^2 = 0

`Ellipsoïde de centre c`

16/33*X^2+4/11*Y^2+8/33*Z^2 = 1

`Quadrique à centre unique, surface non réglée`

`Paramétrage: `, [X = 1/4*33^(1/2)*cos(phi)*cos(theta), Y = 1/2*11^(1/2)*cos(phi)*sin(theta), Z = 1/4*66^(1/2)*sin(phi)], theta = 0 .. 2*Pi, phi = -1/2*Pi .. 1/2*Pi

[Maple Plot]

Exemple 8: Cylindre hyperbolique

>    f:=-x^2-x+y^2-2*y-z^2-z-2*x*z; quadrique(f,[x,y,z]);

f := -x^2-x+y^2-2*y-z^2-z-2*x*z

`Forme quadratique associée:  q` = -2*x*z-z^2+y^2-x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[-1, 0, -1], [0, 1, 0], [-1, 0, -1]])

`Valeur propres de A ` = [-2, 0, 1]

`Matrice diagonale semblable à A:   D` = matrix([[0, 0, 0], [0, -2, 0], [0, 0, 1]])

`Matrice de passage orthogonale:   P` = matrix([[1/2*2^(1/2), 1/2*2^(1/2), 0], [0, 0, 1], [-1/2*2^(1/2), 1/2*2^(1/2), 0]])

`Directions principales de la quadrique:`

`I ` = vector([1/2*2^(1/2), 0, -1/2*2^(1/2)]), ` J ` = vector([1/2*2^(1/2), 0, 1/2*2^(1/2)]), ` K ` = vector([0, 1, 0])

`Equation dans (o,I,J,K): `

-2*Y^2-2^(1/2)*Y+Z^2-2*Z = 0

`nouvelle origine de coordonnées dans [o,I,J,K]:   s` = [0, -1/4*2^(1/2), 1]

`équation dans (s,I,J,K):`

-2*Y^2-3/4+Z^2 = 0

`Cylindre hyperbolique`

-8/3*Y^2+4/3*Z^2 = 1

`Quadrique admettant une droite des centres (l'axe du cylindre), surface réglée`

`Axe du cylindre: (s,I)`

`Paramétrage: `, [X = lambda, Y = 1/4*epsilon*6^(1/2)*cosh(theta), Z = 1/2*3^(1/2)*sinh(theta)], theta = -infinity .. infinity, lambda = -infinity .. infinity, epsilon = `±1`

[Maple Plot]

Exemple 9: Paraboloïde elliptique

>    f:=4*x^2-12*x+12+3*y^2-12*y-9*z; quadrique(f,[x,y,z]);

f := 4*x^2-12*x+12+3*y^2-12*y-9*z

`Forme quadratique associée:  q` = 3*y^2+4*x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[4, 0, 0], [0, 3, 0], [0, 0, 0]])

`Valeur propres de A ` = [0, 3, 4]

`Matrice diagonale semblable à A:   D` = matrix([[0, 0, 0], [0, 3, 0], [0, 0, 4]])

`Matrice de passage orthogonale:   P` = matrix([[0, 0, 1], [0, 1, 0], [1, 0, 0]])

`Directions principales de la quadrique:`

`I ` = vector([0, 0, 1]), ` J ` = vector([0, 1, 0]), ` K ` = vector([1, 0, 0])

`Equation dans (o,I,J,K): `

4*Z^2-12*Z+12+3*Y^2-12*Y-9*X = 0

`nouvelle origine de coordonnées dans [o,I,J,K]:   s` = [-1, 2, 3/2]

`équation dans (s,I,J,K):`

4*Z^2+3*Y^2-9*X = 0

`Paraboloïde elliptique`

3*Y^2+4*Z^2 = 9*X

`Quadrique sans centre, surface non réglée`

`Paramétrage: `, [X = 1/9*lambda^2, Y = 1/3*3^(1/2)*lambda*cos(theta), Z = 1/2*lambda*sin(theta)], theta = 0 .. 2*Pi, lambda = -infinity .. infinity

[Maple Plot]

Exemple 10: Paraboloïde hyperbolique

>    f:=-4*x^2-4*x+5*y+4*z^2+8*z-7; quadrique(f,[x,y,z]);

f := -4*x^2-4*x+5*y+4*z^2+8*z-7

`Forme quadratique associée:  q` = 4*z^2-4*x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[-4, 0, 0], [0, 0, 0], [0, 0, 4]])

`Valeur propres de A ` = [-4, 0, 4]

`Matrice diagonale semblable à A:   D` = matrix([[0, 0, 0], [0, -4, 0], [0, 0, 4]])

`Matrice de passage orthogonale:   P` = matrix([[0, 1, 0], [1, 0, 0], [0, 0, 1]])

`Directions principales de la quadrique:`

`I ` = vector([0, 1, 0]), ` J ` = vector([1, 0, 0]), ` K ` = vector([0, 0, 1])

`Equation dans (o,I,J,K): `

-4*Y^2-4*Y+5*X+4*Z^2+8*Z-7 = 0

`nouvelle origine de coordonnées dans [o,I,J,K]:   s` = [2, -1/2, -1]

`équation dans (s,I,J,K):`

-4*Y^2+5*X+4*Z^2 = 0

`Paraboloïde hyperbolique`

4*Y^2-4*Z^2 = 5*X

`Quadrique sans centre, surface réglée`

`Paramétrage: `, [X = 1/5*lambda^2, Y = 1/2*lambda*cosh(theta), Z = 1/2*lambda*sinh(theta)], theta = -infinity .. infinity, lambda = -infinity .. infinity

[Maple Plot]

Exemple 11: Cylindre parabolique

>    f:=-2*x^2+4*x*y-4*x*z-2*y^2+4*y*z-2*z^2+4*x-5*y+6*z-11; quadrique(f,[x,y,z]);

f := -2*x^2+4*x*y-4*x*z-2*y^2+4*y*z-2*z^2+4*x-5*y+6*z-11

`Forme quadratique associée:  q` = -2*z^2+4*y*z-2*y^2-4*x*z+4*x*y-2*x^2

`Matrice de la forme quadratique associée:`

`A ` = matrix([[-2, 2, -2], [2, -2, 2], [-2, 2, -2]])

`Valeur propres de A ` = [-6, 0, 0]

`Matrice diagonale semblable à A:   D` = matrix([[0, 0, 0], [0, -6, 0], [0, 0, 0]])

`Matrice de passage orthogonale:   P` = matrix([[-1/6*2^(1/2)*3^(1/2), 1/3*3^(1/2), -1/2*2^(1/2)], [1/6*2^(1/2)*3^(1/2), -1/3*3^(1/2), -1/2*2^(1/2)], [1/3*2^(1/2)*3^(1/2), 1/3*3^(1/2), 0]])

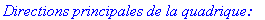
`Directions principales de la quadrique:`

`I ` = vector([-1/6*2^(1/2)*3^(1/2), 1/6*2^(1/2)*3^(1/2), 1/3*2^(1/2)*3^(1/2)]), ` J ` = vector([1/3*3^(1/2), -1/3*3^(1/2), 1/3*3^(1/2)]), ` K ` = vector([-1/2*2^(1/2), -1/2*2^(1/2), 0])

`Equation dans (o,I,J,K): `

-11+5*3^(1/2)*Y+1/2*2^(1/2)*Z-6*Y^2+1/2*2^(1/2)*3^(1/2)*X = 0

`nouvelle origine de coordonnées dans [o,I,J,K]:   s` = [0, 5/12*3^(1/2), 0]

`équation dans (s,I,J,K):`

-63/8+1/2*2^(1/2)*Z-6*Y^2+1/2*2^(1/2)*3^(1/2)*X = 0

`changement de base (coordonnées dans (I,J,K))`

` U` = vector([-1/2, 0, 1/2*3^(1/2)]), ` V` = vector([0, 1, 0]), ` W` = vector([-1/2*3^(1/2), 0, -1/2])

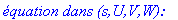
`équation dans (s,U,V,W):`

-63/8-2^(1/2)*Z-6*Y^2 = 0

`nouvelle origine de coordonnées dans [s,U,V,W]:  t` = [0, 0, -63/16*2^(1/2)]

`Cylindre parabolique`

`équation dans (t,U,V,W):`

-2^(1/2)*Z-6*Y^2 = 0

`Quadrique sans centre, surface réglée`

`Paramétrage: `, [X = mu, Y = lambda, Z = -3*lambda^2*2^(1/2)], lambda = -infinity .. infinity, mu = -infinity .. infinity

[Maple Plot]


 

 

 

haut de cette page


©  - Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.