 |
Polynômes
et fractions rationnelles |
|
Page d'accueil Cours Maple << Chapitre précédent Chapitre suivant >> POLYNÔMES:
> restart; Un polynôme a le type polynom , et peut avoir plusieurs variables :
> P:=-7*x+5*x^2+75*x^3;Q:=x*(2*x-3*y)^2*(x-y);
> type(P,polynom),whattype(P),whattype(Q);
nops(P) donne le nombre de termes selon la forme , développée ou factorisée , de P :
> nops(P),nops(Q);
op(P) donne sous forme de séquence les termes ou les facteurs de P :
> op(P);op(Q);
Coefficients , degré , valuation:
> coeff(P,x^3);
> coeff(P,x,3);
Obtenir tous les coefficients de P (valable lorsque P est sous forme développée) > coeffs(P);coeffs(Q);
Error, invalid arguments to coeffs > coeffs(expand(Q));
Coefficient du terme de plus haut (de plus bas) degré: > lcoeff(P),tcoeff(P);
> lcoeff(Q,y),tcoeff(Q,y);
Degré et valuation: > degree(P),degree(Q,x),degree(Q,y);
> ldegree(P),ldegree(Q,x),ldegree(Q,y);
FONCTIONS SUR LES POLYNÔMES:
quo(P,Q,x,'r') : quotient de la division euclidienne de P par Q , variable x , 'r' (optionnel) variable non assignée recevant le reste . > quo(x^5-1,x^2+x+1,x, 'r');r;
rem(P,Q,x,'q') : reste de la division euclidienne de P par Q , variable x , 'q' (optionnel) variable non assignée recevant le quotient . > rem(x^5-1,x^2+x+1,x, 'q');q;
Discriminant: > discrim(x^3+a*x+b,x);
Evaluer, ordonner, transformer un polynôme:
> subs(x=1+2*I,y=I,Q);
Ordonner Q selon les puissances décroissantes de y: > sort(expand(Q),y);
Développer: > expand((x-3*y+a)*(1-a^2+x+y));
Regrouper les monômes de l'expression en l'indéterminée a : > collect((x-3*y+a)*(1-a^2+x+y),a);
Mettre P sous la forme de Hörner: > P;H:=convert(P,horner);
> with(codegen,cost);
Ce qui est moins coûteux en opérations:
> cost(P),cost(H);
Factoriser sur le corps Q des rationnels > factor(x^3+x^2+x+1);
Normaliser: > normal((4*x-3)^2+x-1);
RACINES ET FACTORISATION DES POLYNÔMES:
Valeur approchées des zéros réels ou complexes avec fsolve : > P:=x^3+x+1:fsolve(P);
> fsolve(P,x,complex);
Localiser les zéros réels dans un intervalle de longueur voulue , ici 10^-3 , avec realroot : > realroot(P,0.001);
Calcul des zéros avec solve(P) : > solve(x^4+1);
Par la fonction factor , on peut factoriser sur Q ou sur le corps induit par les coefficients : > factor(x^4-1);
> factor(x^3-I*x-I+1);
Pour obtenir la factorisation complète:
factor
(P,{
> factor(x^4-1,I);
> factor(x^3-x^2+2*x-2);
> factor(x^3-x^2+2*x-2,{I,sqrt(2)});
On peut aussi utiliser Split , qui donne une factorisation complète : > with(PolynomialTools,Split):P:=Split(x^4-1,x);
RootOf désigne ici toute racine du polynôme _Z²+1, on peut simplifier l'écriture en utilisant alias : > alias(alpha=RootOf(_Z^2+1)):P;
Pour calculer les valeurs possibles de alpha : > allvalues(RootOf(_Z^2+1));
La fonction
roots
donne les zéros avec leur ordre de multiplicité: > roots(x^2+1);
On calcule ses zéros sur le corps Q(I) induit par les coefficients: > roots(x^2+1,I);
FRACTIONS RATIONNELLES : de type ratpoly
> F:=(2*x^2+x-3)^2/(x^4-1);numer(F),denom(F);
> simplify(F);
Factorisation sur IR ou C: factorisation sur IR: > factor(F);
factorisation sur C: > factor(F,I);
retour à la forme normale: > normal(%,expanded);
Décomposition en éléments simples sur IR ou C:
convert(F,parfrac,
x
)
décompose en éléments simples la fraction rationnelle F en l'indéterminée
x
.
Décomposition sur IR: > convert(F,parfrac,x);
Décomposition sur C: > convert(F,parfrac,x,I);
Exercice corrigé 5:
Ex 5.1: Décomposer en éléments simples sur
> F:=1/(x^4+1);
> convert(F,parfrac,x);
F n'est pas décomposée. Voyons les racines du dénominateur: > {solve(denom(F))};
On obtient la décomposition sur IR par: > convert(F,parfrac,x,sqrt(2));
On obtient la décomposition sur C par: > convert(F,parfrac,x,{I,sqrt(2)});
Ex 5.2: Soit
Montrer que les zéros du polynôme dérivé P' sont 3 termes consécutifs d'une suite arithmétique.
> P:=X*(X-1)*(X-2)*(X-3):dP:=diff(expand(P),X);
> zeros:=[solve(dP)];
On trie les éléments de la liste par ordre croissant , sort ne fonctionnant pas ici :
>
tri:=proc(L::list) > zeros:=tri(zeros);
On calcule les écarts entre 2 termes consécutifs , la raison est
> for k to nops(zeros)-1 do print(zeros[k+1]-zeros[k]) end do;
Travail dirigé 5:
TD 5.1:
1° La décomposition de F en éléments simples dans R s'écrit:
On réduit les fractions composant G au même dénominateur et on identifie les numérateurs de F et de G . En déduire les valeurs de a,b,c,d,e,f,g .
2° Calculer la décomposition de F en éléments simples dans C
TD 5.2:
L'algorithme de Hörner permet d'écrire P( x ) sous la forme :
Exemple:
Ecrire une procédure PolyHorner(P , x ) permettant d'écrire P( x ) sous cette forme , P étant un polynôme donné de K[ x ] , x étant le nom de la variable .
NB: il est interdit d'utiliser la fonction horner de MAPLE .
Grace à la fonction
cost
, évaluer le coût en opérations nécessaires pour évaluer Q et
|
© - Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.
 n'a aucun zéro sur Q:
n'a aucun zéro sur Q:






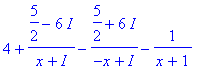





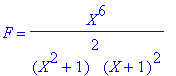

![P(x) = Sum(a[k]*x^k,k = 0 .. n)](images5/chapn576.gif)