 |
Graphisme
avec Maple |
|
Page d'accueil Cours Maple << Chapitre précédent Chapitre suivant >> GRAPHIQUES EN DIMENSION 2:
La fonction
smartplot
constitue la façon la plus simple de représenter une ou plusieurs fonctions
:
> smartplot(cos(2*x)+sin(x),x);
Pour représenter une ou plusieurs fonctions, utiliser plot(f , h , v) ou plot(f, h, v,...) où f : fonction(s) représentée(s) , h et v : intervalle horizontal et vertical (optionnels). La syntaxe la plus simple est plot(f) ou plot(f(x),x=a..b) :
> f:=x->cos(2*x)+sin(x):plot(f(x),x=-2*Pi..2*Pi);
Les arguments restants sont des options que l'on peut spécifier par des équations de la forme option = valeur.
scaling = CONSTRAINED (repère orthonormal) ou UNCONSTRAINED (repère non orthonormal) .Par défaut : UNCONSTRAINED.
axes = Spécifie le type d'axes : FRAMED , BOXED, NORMAL , et NONE.
coords = polar Indique une courbe paramétrique en coordonnées polaires.
numpoints = n Spécifie le nombre minimum de points à être générés (défaut n = 49 ).
resolution = n Spécifie la résolution horizontale en pixels (défaut n = 200 ).
color = n Spécifie la couleur des courbes à tracer .
xtickmarks = n ytickmarks = n Spécifie le nombre de graduations sur l'axe des x ou des y .
style = s Spécifie le style du tracé : par défaut LINE POINT (tracé point par point) , LINE (points reliés par des segments) PATCH (style pour les polygones) , SPLINE (points reliés par une courbe spline)
discont = s Mettre s à la valeur booléenne true pour des fonctions discontinues
title = t Spécifie le titre pour le graphique ( t de type string ).
thickness = n Spécifie l'épaisseur du trait , ( n = 0, 1, 2 , ou 3 , défaut : 0 ).
linestyle = n Spécifie le motif des lignes tracées (lignes pleines : 0 et 1, d'autres valeurs plus grandes donnent des pointillés par exemple).
symbol = s Spécifie le symbole de représentation d'un point : BOX, CROSS, CIRCLEPOINT, et DIAMOND.
font = liste Polices des caractères affichés . liste est une liste [famille, style, taille] , famille : TIMES, COURIER, HELVETICA, SYMBOL. Pour TIMES, le style est ROMAN, BOLD, ITALIC ou BOLDITALIC. Pour HELVETICA et COURIER style omis ou BOLD, OBLIQUE, ou BOLDOBLIQUE. Pour SYMBOL , pas de style .
titlefont = liste , axesfont = liste , labelfont = l iste Polices des caractères affichés pour le titre,les graduations des axes,les légendes des axes (pour liste , voir font = liste).
view=[xmin .. xmax,ymin .. ymax] Spécifie la zone de dessin à représenter à l'écran .
Représenter un ensemble de plusieurs courbes:
> plot({sin(x),x, x-x^3/6}, x=-2..2,thickness=2,scaling=CONSTRAINED);
Intervalle à borne infinie: > plot(sin(x)/x, x=0..infinity);
Représenter des points: on donne la liste des coordonnées, abscisse puis ordonnée. > plot([[0,0],[1,1],[2,1],[2,0],[1,-1],[0,0]], x=0..2, style=point);
Représenter des lignes brisées: même principe que pour les points, en enlevant style=point . > plot([[0,0],[1,1],[2,1],[2,0],[1,-1],[0,0]], x=0..2);
Courbe en coordonnées polaires: plot([r(t),theta(t),t=a..b],coords=polar,...) > plot([sin(4*t),t,t=-2*Pi..2*Pi],coords=polar,thickness=2,font=[HELVETICA,BOLD,8],title="R=sin 4t",color=red);
On obtient le même résultat en utilisant la fonction polarplot du package plots : > with(plots):polarplot([sin(4*t),t,t=-2*Pi..2*Pi],thickness=2,font=[HELVETICA,BOLD,8],title="R=sin 4t",color=red);
Courbe paramétrée: plot([x(t),y(t),t=a..b],...)
> plot([cos(2*t)+2*cos(t),sin(2*t),t=0..2*Pi],color=blue);
OUTILS 2D DU PACKAGE plots:
Le package plots fournit d'autres outils graphiques pour la dimension 2 :
> with(plots);
Citons , entre autres :
La fonction animate , qui permet de créer des animations dans une fenêtre dont la barre d'outils comporte des touches identiques à celles d'un lecteur de cassettes : Exemple: famille de paraboles dépendant de m > animate(m*x^2,x=-3..3,m=-10..10);
Tracer des courbes définies implicitement sous la forme f(x,y)=0 avec implicitplot > implicitplot(x^3+x-y^2+1=0,x=-10..10,y=-10..10);
Visualiser un champ de vecteurs avec fieldplot , ( arrows = LINE,SLIM,THIN ou THICK) > fieldplot([x*x-y*y,2*x+y^3],x=-1..1,y=-1..1,arrows=SLIM);
gradplot permet de visualiser un champ de gradients .
logplot , loglogplot donnent une graduation logarithmique sur l'axe des y ou les 2 axes
odeplot permet de tracer les courbes intégrales d'une équation différentielle.
textplot permet d'écrire sur un dessin .
densityplot et contourplot permettent de tracer respectivement des graphes de densité ou des courbes de niveau.
display permet de représenter plusieurs objets graphiques de nature éventuellement différentes sur un même graphique. L'option insequence=true permet de le transformer en animation.
Exemple:
tracé du cercle c de centre O de rayon 1, de la droite d:
d'équation
>
c:=plot([cos(t),sin(t),t=0..2*Pi],color=blue):
GRAPHIQUES EN DIMENSION 3:
La fonction
smartplot3d
constitue la façon la plus simple de représenter une ou plusieurs surfaces
:
> smartplot3d(exp(-(x^2+y^2)));
plot3d(f(x,y),x=a..b,y=c..d,...) ou plot3d(f,a..b,c..d,...) permettent de tracer une surface. > f:=(x,y)->exp(-(x^2+y^2)):plot3d(f,-1..1,-1..1,axes=BOXED,orientation=[-45,60],numpoints =1000,color=blue);
Comme pour la dimension 2 , on retrouve les options axes , scaling , tickmarks , title , view , numpoints (par défaut 625) et :
labels = [`x`,`y`,`z`]
orientation = [theta,phi] précise les angles de vision en coordonnées sphériques .
projection = r , avec r réel de [0,1] . FISHEYE=0 , NORMAL=0.5 , ORTHOGONAL=1.
grid = [m,n] détermine la grille rectangulaire m x n (par défaut 25 x 25)
style = s ( où s parmi POINT,HIDDEN,PATCH,WIREFRAME,CONTOUR, PATCHNOGRID,PATCHNOCONTOUR,LINE . Par défaut : HIDDEN )
ambientlight = [r,v,b] fixe l'intensité des couleurs rouge,vert,bleu (valeurs dans [0,1]) .
colour = c fixe la couleur à c .
light = [phi,theta,r,v,b] fixe l'éclairage de la surface selon les angles phi,theta en coordonnées sphériques avec les couleurs r,v,b .
shading = s ( où s parmi XYZ,XY,Z,ZGREYSCALE,ZHUE,NONE ) pour préciser la façon dont la surface est coloriée .
coords = c ( ou c parmi cartesian,spherical,cylindrical )
Les surfaces peuvent être paramétrées :
> plot3d([(4+sin(t))*cos(u),(4+sin(t))*sin(u),2*sin(t)],t=0..2*Pi,u=0..2*Pi,axes=framed,shading=ZHUE,ambientlight =[0.85,0.75,0.1]);
> plot3d(z,theta=0..2*Pi,z=0..2,coords=cylindrical,title="Un cône");
> plot3d(5,theta=0..2*Pi,phi=0..Pi,axes=BOXED,coords=spherical,scaling=constrained,color=blue,title="Une sphère");
OUTILS 3D DU PACKAGE plots:
Le package plots fournit d'autres outils graphiques pour la dimension 3 :
> with(plots);
Citons entre autres :
animate3d , pour créer des animations graphiques .
fieldplot3d , gradplot3d pour visualiser un champ de vecteurs ou de gradients .
display3d permet de représenter plusieurs objets graphiques de nature éventuellement différentes sur un même graphique. L'option insequence=true permet de le transformer en animation.
polyhedraplot pour représenter des polyèdres : polyscale = n (taille du polyèdre) polytype parmi tetrahedron,octahedron,hexahedron,dodecahedron,icosahedron.
> polyhedraplot([0,0,0],polyscale=10,polytype = icosahedron,scaling=CONSTRAINED,axes=BOXED,title="Icosaèdre");
Tracé de surfaces implicites ou de courbes gauches: > implicitplot3d(x^2+y^2/4+z^2/4-1=0,x=-1..1,y=-2..2,z=-2..2,title="ellipsoide",color=red);
> spacecurve([cos(t),sin(t),t],t=-4*Pi..4*Pi,numpoints=500,axes=FRAMED,title="Courbe gauche : une hélice",color=black);
Exercice corrigé 6:
Soit
S
la surface d'équation cartésienne
1° Représenter S à partir de son équation implicite , pour z variant entre -1 et 1.
2° Définir S à partir d'une représentation paramétrique et représenter alors S .
> with(plots):implicitplot3d(x^2+y^2-z^2-1,x=-sqrt(2)..sqrt(2),y=-sqrt(2)..sqrt(2),z=-1..1,color=blue);
> S:=[cosh(phi)*cos(theta),cosh(phi)*sin(theta),sin(phi)]:plot3d(S,phi=-arcsinh(1)..arcsinh(1),theta=0..2*Pi,color=blue);
Travail dirigé 6:
TD 6.1: régulier à n côtés, de centre (0,0) et de rayon 1: > polygone_regulier(8);
TD 6.2:
une fonction sphere des 4 variables x,y,z,R .
2° Représenter sur un même graphique les sphères
(0,3,0) et (0,0,0) et de rayons respectifs 2,2,1.
|
© - Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.
![[Maple Plot]](images6/chapn61.gif)
![[Maple Plot]](images6/chapn62.gif)
![[Maple Plot]](images6/chapn63.gif)
![[Maple Plot]](images6/chapn64.gif)
![[Maple Plot]](images6/chapn65.gif)
![[Maple Plot]](images6/chapn66.gif)
![[Maple Plot]](images6/chapn67.gif)
![[Maple Plot]](images6/chapn68.gif)
![[Maple Plot]](images6/chapn615.gif)
![[Maple Plot]](images6/chapn616.gif)
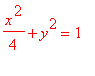 ,dans un même repère orthonormal.
,dans un même repère orthonormal.
![[Maple Plot]](images6/chapn619.gif)
![[Maple Plot]](images6/chapn620.gif)
![[Maple Plot]](images6/chapn621.gif)
![[Maple Plot]](images6/chapn622.gif)
![[Maple Plot]](images6/chapn623.gif)
![[Maple Plot]](images6/chapn624.gif)
![[Maple Plot]](images6/chapn631.gif)
![[Maple Plot]](images6/chapn632.gif)
![[Maple Plot]](images6/chapn633.gif)
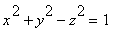 (hyperboloide de révolution à une nappe)
(hyperboloide de révolution à une nappe)
![[Maple Plot]](images6/chapn635.gif)
![[Maple Plot]](images6/chapn636.gif)
![[Maple Plot]](images6/chapn637.gif)