 |
Maple en
analyse |
|
Page d'accueil Cours Maple << Chapitre précédent Chapitre suivant >> FONCTIONS NUMÉRIQUES:
Domaine de définition: la fonction singular permet de déterminer les singularités de certaines fonctions:
>
restart;
Continuité: la fonction iscont permet de déterminer la continuité de certaines fonctions. closed signifie que l'intervalle est fermé.MAPLE travaille par défaut sur des intervalles ouverts.
> iscont(tan(x),x=-Pi/2..Pi/2,closed);
> iscont(tan(x),x=-Pi/2..Pi/2);
Image d'une réunion d'intervalles fermés , avec la fonction evalr : > evalr((x->x^2)(INTERVAL(-1..-0.5)));
Extrema d'une fonction , avec les fonctions minimize et maximize : > minimize(x^2+x-3),maximize(-x^4+x^2+1);
Fonctions définies par intervalles:
> f:=piecewise(x<0,exp(x),x<=4,x/4+1,2);
> plot(f(x),x=-4..8);
Limites: avec la fonction limit(expr, x=a , option) option = left , right .
> limit(sin(x)/x,x=0);
> limit(1/x^3,x=0);
Utilisation de la forme inerte Limit : > Limit(1/x^3,x=0,right) = limit(1/x^3,x=0,right);
Etude locale: avec taylor(expr , x=a , n) pour les développements limités ou de Taylor, series(expr , x=a , n) ou asympt(expr , x , n) pour des développements asymptotiques plus généraux. L'ordre n est facultatif et vaut 6 par défaut .
> taylor(sin(x),x); # a=0 par défaut
> taylor(x^2/(x^2+1),x=infinity,10);
> series(exp(x)/x,x,9); # a=0 par défaut
> asympt(ln(x+1/x),x,7); # toujours en plus l'infini
> asympt(Sum(1/k,k=1..n)-ln(n),n,10); # la constante d'Euler gamma
> evalf(gamma);
leadterm donne le terme principal d'une série: > series(leadterm(sin(x^3)/(2*x)),x=0);
Conversion en polynôme de Taylor: > P:=convert(taylor(exp(x),x=0,5),polynom);
Dérivation: Pour dériver une fonction , utiliser diff(expr,v1,v2,...,vn) qui calcule la dérivée partielle de expr par rapport aux variables v1,v2,...,vn .
> Diff(x/(x^2+y^2),x,y)=diff(x/(x^2+y^2),x,y); # équivaut à Diff(x/(x^2+y^2),x,y): % = value(%);
Noter l'absence de parenthèses dans l'écriture du premier membre . On peut utiliser l'opérateur $ pour éviter de répéter plusieurs fois une variable :
> Diff(x/(x^2+y^2),x$2,y) : % = value(%);
Opérateur différentiel D:
D(
f
) retourne la fonction dérivée première de
f
> D(sin),(D@@2)(sin);
> D(x->x*sin(x)-x);
> f:=(x,y,z)->x^2-3*x*y*z+z^4;
fonction dérivée par rapport à x,y , et z respectivement : > D[1](f);D[2](f);D[3](f);
D[i,j](f) équivaut à D[i](D[j](f)) : > D[1,2](f);
SUITES ET SÉRIES:
Suites définies par des sommes ou des produits:
> Sum(k^2,k=1..n) : % = factor(value(%));
> Product(k/(k+1),k=1..n) : % = simplify(value(%));
Développement asymptotique de la somme partielle d'une série: > series(sum(1/k^2,k=1..n),n=infinity);
Suites récurrentes:
Type
Exemple:
>
f:=x->cos(x):n:=15:u[0]:=-1:
On peut représenter graphiquement la convergence de la suite en construisant une liste T formée des points (u(0),0) , (u(0),u(1)) , (u(1),u(1)) , (u(1),u(2)) , etc...
>
T:=array(1..4*n,[u[0],0,u[0],f(u[0])]):
Type
Exemple:
>
u[0]:=1:v[0]:=4:n:=15:
Type
Exemple:
>
u[0]:=0:u[1]:=4:n:=15:
Résolution de récurrences , avec la fonction rsolve .
Une suite arithmétique de raison -3: > restart:rsolve(w(n+1) = w(n)-3,w);
Une suite géométrique avec condition initiale: > rsolve({w(n+1)=w(n)/3,w(0)=-7},w);
La suite de Fibonacci: > rsolve({fib(n+2)=fib(n+1)+fib(n),fib(0)=0,fib(1)=1},fib);
Séries numériques:
Somme d'une série de Riemann convergente: > sum(1/k^2,k=1..infinity);
La série harmonique est divergente: > sum(1/k,k=1..infinity);
Calcul de la somme d'une série de fonctions > Sum(sin(x)^k,k=1..infinity)=sum(sin(x)^k,k=1..infinity);
Le package powseries contient des fonctions mettant en jeu les séries entières: Consulter les pages d'aide de powseries pour plus de précision. > with(powseries);
> sh := evalpow( sinh(x) ): tpsform(sh, x, 9);
INTÉGRATION:
Le calcul des primitives et des intégrales se fait avec la fonction int . Syntaxes: int(expr , x) et int(expr, x=a..b) .
>
Int(x/(x^4+1),x)=int(x/(x^4+1),x);
> Int(x/(x^4+1),x=0..1) : % = value(%);
Intégrale généralisée convergente: > Int(x/(x^4+1),x=0..infinity) : % = value(%);
Intégrale généralisée divergente: > Int(exp(x)/x,x=1..infinity) : % = value(%);
Le package inttrans contient quelques outils pour la transformation d'intégrales. Consulter les pages d'aide de inttrans pour plus de précision.
> with(inttrans);
La transformée de Laplace de f est définie par
> laplace(sin(omega*t), t, s);
Quelques outils du package student :
> with(student);
Changement de variables dans les intégrales: changevar(eq , intégrale , u) eq est l'équation du changement de variable de la forme f(x)=g(u) , intégrale est l'intégrale et u la nouvelle variable d'intégration :
> J:=Int(t/((t^2+1)*sqrt(1-t^4)),t=0..1);
> changevar(t^2=u,J,u):% = value(%);
Intégration par parties , avec la fonction intparts(intégrale,u) , u est le facteur à dériver.
> J:=Int(x^2*arccos(x),x):intparts(J,arccos(x));
> J:=value(%);
METHODES D'APPROXIMATION D'INTEGRALES:
METHODE DES RECTANGLES: On découpe [a,b] en n intervalles de même longueur extrémité gauche : représentation avec leftbox(expr,x=a..b,n) , calcul avec leftsum(expr,x=a..b,n)
extrémité droite : représentation avec rightbox(expr,x=a..b,n) , calcul avec rightsum(expr,x=a..b,n)
point médian : représentation avec middlebox(expr,x=a..b,n) , calcul avec middlesum(expr,x=a..b,n)
METHODE DES TRAPEZES: calcul avec trapezoid(expr,x=a..b,n)
METHODE DE SIMPSON: calcul avec simpson(expr,x=a..b,n) , avec n pair.
Exemple:
avec f:
> middlebox(exp(-x^2),x=-1..1,20);middlesum(exp(-x^2),x=-1..1,20);evalf(%);
> evalf(trapezoid(exp(-x^2),x=-1..1,20));
> evalf(simpson(exp(-x^2),x=-1..1,20));
Calcul d'intégrales doubles ou triples:
> Doubleint(x^3*y-x^2-y*x,x=-a..a,y=-b..b):%=value(%);
> Tripleint(x*y*z*sin(x+y+z),x=0..Pi,y=-Pi..Pi,z=0..Pi):%=value(%);
ÉQUATIONS ET SYSTÈMES DIFFÉRENTIELS:
Equations du premier ordre: MAPLE sait résoudre directement les équations de type classique - linéaire - avec facteur intégrant - séparable - homogène - résolue en x - de Bernoulli - de Clairaut - de Riccati .
> restart:eq:=diff(y(x),x)+3*y(x)=exp(-x):dsolve(eq,y(x));
_C1 désigne une constante réelle arbitraire.
La même avec la condition initiale
> dsolve({eq,y(0)=1.5},y(x));
Les solutions y(x) ne sont pas directement utilisables : en assignant la solution à y(x) on peut utiliser le résultat , par exemple pour représenter les courbes intégrales :
> assign(dsolve(eq,y(x))):y:=unapply(y(x),_C1,x);
> plot({seq(y(_C1,x),_C1=-3..3)},x=-5..5,y=-20..20);
On peut préciser des options de résolution : explicit (pour tenter d'exprimer la solution comme fonction explicite de la variable) , series (chercher les solutions sous forme de séries)
>
eq:={diff(z(x),x)+z(x)*cos(x)=1,z(0)=1}:
>
with(plots,odeplot):
Equations du second ordre: MAPLE sait résoudre directement les équations de type classique - linéaire - d'Euler - de Bessel .
> restart:eq2:=diff(y(t),t$2)+diff(y(t),t)+y(t)=t;
> dsolve(eq2,y(t));
La même avec conditions initiales: > dsolve({eq2,y(0)=0,D(y)(0)=-1},y(t));
Les options de résolution sont les mêmes qu'à l'ordre 1.
Systèmes différentiels:
Exemple: résoudre x ' =x- 2 y , y ' = 2 x+ 3 y . Représenter la solution vérifiant x (0) = 0 et y( 0) = 1 .
>
restart:sys:=diff(x(t),t)=x(t)-2*y(t),diff(y(t),t)=2*x(t)+3*y(t):
>
p:=dsolve({sys,x(0)=0,y(0)=1},{x(t),y(t)},numeric):
Résolution d'équations aux dérivées partielles:
> edp:=y*diff(U(x,y),x)+x*diff(U(x,y),y)=0;
> pdsolve(edp,U(x,y) );
_F1 désigne une fonction arbitraire de classe C1 de la variable
Travail dirigé 7:
Soit f la fonction définie pour tout réel
x
>0
par
1° Etablir les singularités de la fonction f et vérifier sa continuité.
2° Etudier les limites de f aux bornes des intervalles composant Df. Quelle est l'asymptote de la courbe Cf de f ?
3° Calculer f '( x ) et étudier son signe ( on aura recours à une fonction auxiliaire g ).
4° Représenter la courbe Cf.
5° Etudier la dérivabilité du prolongement par continuité de f aux points 0 et 1.
|
© - Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.
![f := PIECEWISE([exp(x), x < 0],[1/4*x+1, x <= 4],[2...](images7/chapn76.gif)
![[Maple Plot]](images7/chapn77.gif)
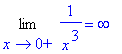
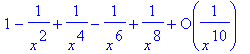
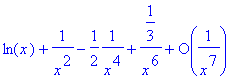
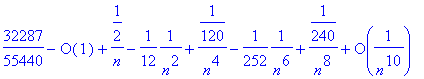
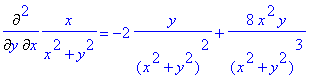
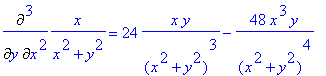
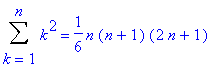
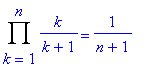
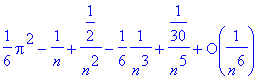
![[Maple Plot]](images7/chapn735.gif)
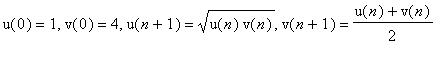 .
.
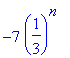
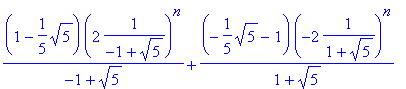
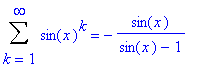
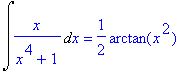
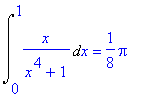
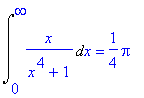
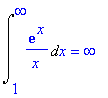
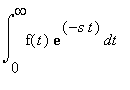 .
.
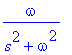
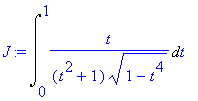
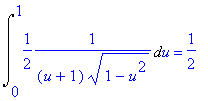
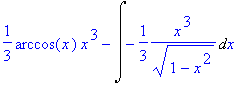
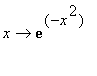
![[Maple Plot]](images7/chapn766.gif)
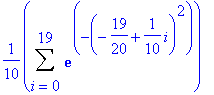
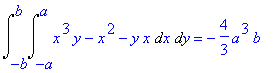
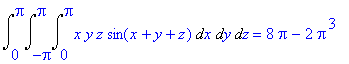
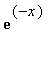
![[Maple Plot]](images7/chapn778.gif)
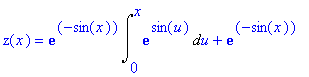
![[Maple Plot]](images7/chapn781.gif)
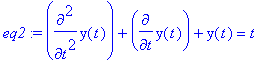
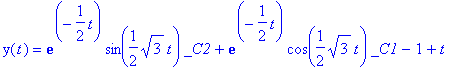
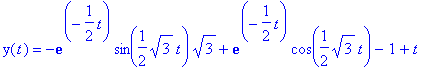
![[Maple Plot]](images7/chapn787.gif)
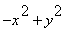 .
.
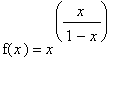 .
.