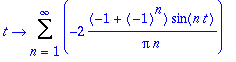Page d'accueil   Thèmes d'activités   << Thème précédent   Thème suivant >>

Corrigé du thème

> restart;

f est une fonction périodique de classe C1 par morceaux sur IR, à valeurs dans IR..

Paramètres formels passés à la procédure Serie_Fourier:

T : période de f .
subdivision : subdivision de l'intervalle [- T /2 , T /2].
liste_fonction : définition de f sur chacun des intervalles de la subdivision précédente.
t : nom de la variable.

Variables locales exportées par le module créé par Serie_Fourier:
periode : T .

pulsation : .
a ( n ), b ( n ): coefficients de Fourier réels et de f .

c ( n ): coefficients de Fourier exponentiels de f .

Harmonique ( n :: nonnegint) : rend le n -ième harmonique .
graphe ( Nmin :: nonnegint, Nmax :: nonnegint, a , b ) :

Nmin , Nmax : ordre minimum et maximum des harmoniques souhaités.
a , b : entier minimum et maximum( ... la valeur -1 correspond à [-3* T /2 , - T /2] , la valeur 0 correspond à [- T /2 , T /2],

la valeur 1 correspond à [ T /2 , 3* T /2] etc ...)
La procédure graphe représente f et les harmoniques correspondant aux entiers de Nmin à Nmax ,

sur l'intervalle [- T /2+ a * T , T /2+ b * T ]
serieR () : rend la série de Fourier (coefficients réels) de f , définie par .

serieC () : rend la série de Fourier (coefficients complexes) de f , définie par .

Parseval () : rend l'identité de Parseval , définie par +

Procédures locales de la procédure Serie_Fourier:

integrale ( ) : calcule l'intégrale de la fonction sur [0, T ] .

def : définition de f en une seule formule à partir des intervalles de la subdivision de [- T /2 , T /2]

Corrigé:

Énoncé du thème

> Serie_Fourier:=proc(T,subdivision::list,liste_fonction::list,t::name)
        

    module()

        description "Ce module comporte des outils sur les séries de Fourier";
        option `Copyright (c) Octobre 2001 A.Le Stang`;
        export periode, pulsation, a, b, c,
                        harmonique, graphe, serieR, serieC, Parseval;
        local p,q,integrale,def;
            periode := T;
            pulsation := 2*Pi/T;
            p:=nops(subdivision);q:=nops(liste_fonction);
            if q<>p-1 or subdivision[1]<>-T/2 or subdivision[p]<>T/2
            then error "Paramètres non conformes" end if;


integrale:=proc(phi)
    local i,s;
    s:=0;
    for i to nops(liste_fonction) do
        s:=s+int(liste_fonction[i](t)*phi(t),t=subdivision[i]..subdivision[i+1]);
    end do;
    s;
end proc;

a:=proc(n)
    local i,cond,T,w;
    T:=periode;
    w:=pulsation;
    i:=1/T*integrale(unapply(cos(n*w*t),t));
    if n=0 then return(i) end if;
    if type(n,name) then
        cond:=cos(n*Pi)=(-1)^n,sin(n*Pi)=0,((-1)^n)^2=1,cos(n*Pi/2)=0:
        factor(subs(cond,2*i));
    else 2*i end if;
end proc;

b:=proc(n)
    local i,cond,T,w;
    T:=periode;
    w:=pulsation;
    i:=2/T*integrale(unapply(sin(n*w*t),t));
    if type(n,name) then
        cond:=cos(n*Pi)=(-1)^n,sin(n*Pi)=0,((-1)^n)^2=1,cos(n*Pi/2)=0:
        factor(subs(cond,i));
    else i end if;
end proc;

c:=proc(n)
    local i,cond,T,w;
    T:=periode;
    w:=pulsation;
    i:=1/T*integrale(unapply(exp(-I*n*w*t),t));
    if n=0 then return(i) end if;
    if type(n,name) then         
        cond:=exp(I*n*Pi)=(-1)^n,exp(-I*Pi*n)=(-1)^n,exp(2*I*n*Pi)=0,((-1)^n)^2=1:             factor(subs(cond,i));
    else i end if;
end proc;

harmonique:=proc(n::nonnegint)
    local sf,k,w;
    w:=pulsation;
    sf:=array(0..n);
    sf[0]:=unapply(a(0),t);
    if n=0 then return sf[0] end if;
    for k from 1 to n do
        sf[k]:=unapply(sf[k-1](t)+a(k)*cos(k*w*t)+b(k)*sin(k*w*t),t);
    end do;
end proc;

def:=proc()
    local i,s;
    s:=0;
    for i to nops(liste_fonction) do  s:=s+(Heaviside(t-subdivision[i])-Heaviside(t-subdivision[i+1]))*liste_fonction[i](t)
    end do;
    s:=unapply(s,t);
end proc;

graphe:=proc(Nmin::nonnegint,Nmax::nonnegint,a, b)
    local i,s,F,CF,CH,T;
    if a>b or Nmin>Nmax then error "Paramètres non conformes" end if;
    T:=periode;
    F:=def();
    s:=0;
    for i from a to b do
        s:=s+F(t-i*T)
    end do;
    F:=unapply(s,t);
    CF:=plot(F(t),t=-T/2+a*T..T/2+b*T,thickness=2,color=black):             
    CH:=plot({seq(harmonique(i)(t),i=Nmin..Nmax)},t=-T/2+a*T..T/2+b*T):
    plots[display]({CF,CH});
end proc;

serieR:=proc()
    local n,w;
    w:=pulsation;     
    unapply(a(0)+Sum(a(n)*cos(n*w*t)+b(n)*sin(n*w*t),n=1..infinity),t);
end proc;

serieC:=proc()
    local n,w;
    w:=pulsation; unapply(Sum(c(n)*exp(I*n*w*t),n=-infinity..infinity),t);
end proc;

Parseval:=proc()
    local i,k,L,T,n;
    T:=periode;
    L:=map(t->t^2,liste_fonction);
    i:=0;
    for k to nops(L) do
        i:=i+int(L[k](t),t=subdivision[k]..subdivision[k+1]);
    end do;
    1/T*i=a(0)^2+1/2*Sum(a(n)^2+b(n)^2,n=1..infinity);
end proc;

end module;

end proc;

Premier exemple:

> Sf:=Serie_Fourier(2*Pi,[-Pi,0,Pi],[t->-1,t->1],t):

> Sf:-periode;

> Sf:-pulsation;

> Sf:-a(0);

> Sf:-a(n);

> Sf:-b(n);

> Sf:-c(n);

> Sf:-harmonique(9);

> Sf:-graphe(1,9,-1,1);

> Sf:-serieR();

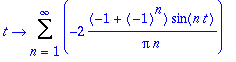
> Sf:-serieC();

> Sf:-Parseval();

Deuxième exemple: est un réel non entier.

> Sf:=Serie_Fourier(2*Pi,[-Pi,Pi],[t->cos(alpha*t)],t):

> Sf:-periode;

> Sf:-pulsation;

> Sf:-a(0);

> Sf:-a(n);

> Sf:-b(n);

> Sf:-c(n);

> Sf:-harmonique(3);

La série de Fourier de f coïncide avec f sur [ ] :

> cos(alpha*t) = Sf:-serieR()(t);

> Sf:-serieC()(t);

Troisième exemple:

> Sf:=Serie_Fourier(2*Pi,[-Pi,0,Pi],[t->-t*(2*Pi+t),t->t*(2*Pi-t)],t):

> Sf:-periode;

> Sf:-pulsation;

> Sf:-a(0);

> Sf:-a(n);

> Sf:-b(n);

> Sf:-c(n);

> Sf:-harmonique(5);

La série de Fourier de f coïncide avec f sur [ ]:

> t*(2*Pi-t) = expand(Sf:-serieR()(t));

> eq:=expand(-1/4*subs(t=0,%)):isolate(eq,op(2,rhs(%)));

> expand(Sf:-Parseval());

> eq:=expand(1/8*%):isolate(eq,op(2,rhs(%)));

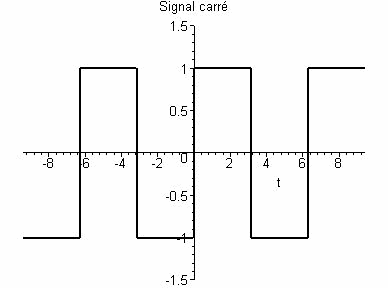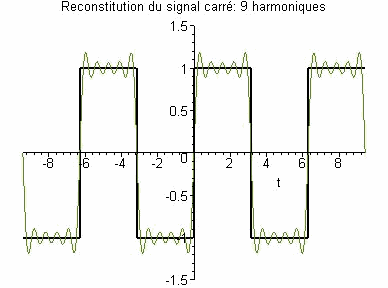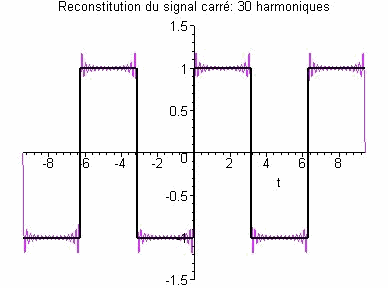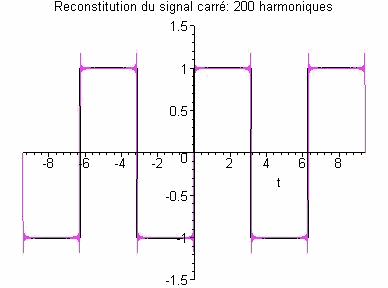
Reconstitution d'un signal carré à l'aide de séries de Fourier:

haut de cette page