|
Page d'accueil
Thèmes d'activités
<< Thème précédent
Thème suivant >>
On se propose dans cette feuille de calcul
de transformer en notation polonaise inversée
(NPI) une expression mathématique donnée sous
forme de chaîne de caractères.
Par exemple, l'expression a+b*c
s'écrira en NPI: abc*+
. Cette notation polonaise est utilisée par les
calculatrices Hewlett-Packard.
Dans un second temps, la formule obtenue
en NPI sera évaluée en utilisant le concept de pile (
stack en anglais).
Les éléments constitutifs d'une expression
mathématique sont:
- les
opérateurs : ce sont les symboles des quatre
opérations élémentaires "+", "-", "*", "/", le symbole de la puissance "^" et
le symbole "+-" désignant l'opérateur unaire de changement de signe.
- les
séparateurs : ce sont les opérateurs auxquels
on adjoint les symboles : "," (virgule) , "(" (parenthèse ouvrante) et ")"
(parenthèse fermante).
- les fonctions prédéfinies
: à une variable (Functions1) comme "abs" ou "trunc", ou à
deux variables (Functions2) comme "min" ou "max". On pourrait en rajouter
d'autres si besoin est.
|
> |
Operators:={"+","-","*","/","^","+-"}; Separators:=Operators union {",",
"(", ")"};
Functions1:={"abs","sqrt","ln","exp","sin","cos","tan","floor","ceil","trunc"};
Functions2:={"min","max"}; Functions:=Functions1 union Functions2;
|
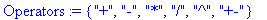
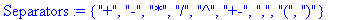
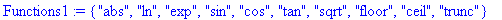
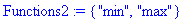

- les
fonctions-utilisateur : définies par
l'utilisateur, à une variable (UserFunctions1) comme ici "ch" ou à deux
variables (UserFunctions2) comme ici "logbase".
|
> |
ch:=x->(exp(x)+exp(-x))/2;
#fonction-utilisateur à une variable (cosinus hyperbolique de x)
logbase:=(a,x)->ln(x)/ln(a);
#fonction-utilisateur à 2 variables (log en base a de x)
UserFunctions1:={"ch"}; UserFunctions2:={"logbase"};
UserFunctions:=UserFunctions1 union UserFunctions2;
|
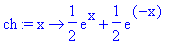
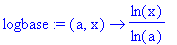

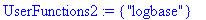
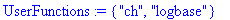
La priorité des opérateurs est donnée par
la table Prec ( order of precedence
en anglais). De la moins prioritaire (1 pour "+" ou "-")
à la plus prioritaire (3 pour "^" ou "+-").
Les fonctions ont aussi une priorité 3.
|
> |
Prec:=table(["+" = 1,
"-" = 1, "*"=2, "/"=2, "^"=3, "+-"=3]);
for k in Functions do Prec[k]:=3 od: for k in UserFunctions do Prec[k]:=3
od: |
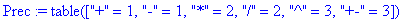
|
> |
Prec["+"], Prec["/"],
Prec["sqrt"], Prec["logbase"];
|
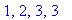
L'associativité gauche, droite des
opérateurs est donnée par la table Assoc (valeur
left ou
right ). "+-" n'est pas
concernée (valeur no
) .
|
> |
Assoc:=table(["+" =
left, "-" = left, "*"=left, "/"=left, "^"=right, "+-"=no]);
|
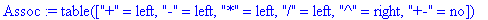
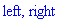
La procédure
RemoveChar (
c :: string,
s :: string) donne pour
résultat la chaîne de caractères obtenue en supprimant le caractère
c de la chaîne de
caractères s .
|
> |
RemoveChar:=proc(c::string,s::string)
local k,t:
t:="":
for k to length(s) do
if s[k]<>c then t:=cat(t,s[k]) end if
end do;
t
end proc:
|
|
> |
RemoveChar(" ","To be
or not to be"); |

La procédure
GetInteger (
s :: string,
n :: nonnegint) retourne
la valeur de l'entier obtenue à partir de la position
n dans la chaîne de
caractères s.
Le format scientifique, par exemple ici 012345.67E-04 sera reconnu: on obtient
le résultat 12345.
|
> |
GetInteger:=proc(s::string,n::nonnegint)
global indx;
local intg,n1;
if IsDigit(s[n]) then
n1:=n; indx:=n:
intg:=Ord(s[n1])-Ord("0");
while s[n1+1]<>"" and IsDigit(s[n1+1]) do
n1:=n1+1: indx:=indx+1: intg:=10*intg+Ord(s[n1])-Ord("0") end do;
intg
else error "number expected at position " || n end if
end proc:
|
|
> |
s:="abc+012345.67E-04*x": GetInteger(s,5);
|
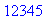
La procédure
GetNumber (
s :: string,
n :: nonnegint) retourne
une séquence de la forme chaine
, valeur
obtenue à partir de la position
n dans la chaîne
de
caractères s.
Par exemple ici à partir de la position 1, on obtient:
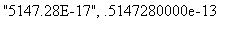 .
.
|
> |
GetNumber:=proc(s::string,n::nonnegint)
global indx;
local intg1,intg2,intg3,n1;
n1:=n; indx:=n:
intg1:=GetInteger(s,n1):
n1:=indx: intg2:=0: intg3:=0:
if s[n1+1]="." then
if IsDigit(s[n1+2]) then n1:=n1+2: intg2:=GetInteger(s,n1): n1:=indx: end
if
end if;
if s[n1+1]="e" or s[n1+1]="E" then
if s[n1+2]="-" and IsDigit(s[n1+3]) then
n1:=n1+3: intg3:=GetInteger(s,n1): intg3:=-intg3
elif s[n1+2]="+" and IsDigit(s[n1+3]) then
n1:=n1+3: intg3:=GetInteger(s,n1)
else
if IsDigit(s[n1+2]) then
n1:=n1+2: intg3:=GetInteger(s,n1)
end if
end if:
end if;
s[n..indx],(intg1+intg2/10.^length(intg2))*10.^intg3
end proc:
|
|
> |
GetNumber("5147.28E-17-2*max(ln(8)+1 , 7 / 5)) /(3+2^6 ) ",1);
|
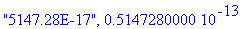
La procédure
GetIdentifier (
s :: string,
n :: nonnegint)
retourne une chaîne de caractères de type
identificateur (de fonction ou de variable)
obtenue à partir de la position n
dans la chaîne de caractères s.
Un identificateur
commence par une lettre, suivie de lettres ou de chiffres
(comme par exemple ici "abc1").
|
> |
GetIdentifier:=proc(s::string,n::nonnegint)
global indx;
local n1,ch;
n1:=n; indx:=n: ch:=s[n]:
while s[n1+1]<>"" and IsAlphaNumeric(s[n1+1]) do
n1:=n1+1: indx:=indx+1: ch:=cat(ch,s[n1])
end do;
ch
end proc:
|
|
> |
s:="125-abc1+012345.67E-04*x": GetIdentifier(s,5);
|
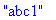
Procédures retournant l'index du nom d'une
fonction dans leur table respective (si le nom n'est pas présent dans la table,
le résultat est 0):
|
> |
GetFunction1:=proc(s::string)
global Functions1;
local i;
if member(s,Functions1,'i') then i else 0 end if;
end proc:
|
|
> |
GetFunction2:=proc(s::string)
global Functions2;
local i;
if member(s,Functions2,'i') then i else 0 end if;
end proc:
|
|
> |
GetUserFunction1:=proc(s::string)
global UserFunctions1;
local i;
if member(s,UserFunctions1,'i') then i else 0 end if;
end proc:
|
|
> |
GetUserFunction2:=proc(s::string)
global UserFunctions2;
local i;
if member(s,UserFunctions2,'i') then i else 0 end if;
end proc:
|
|
> |
GetFunction1("max"),
GetFunction1("tan"), GetFunction2("ln"), GetFunction2("max");
|
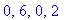
|
> |
GetUserFunction1("tan"), GetUserFunction1("ch"), GetUserFunction2("max"),
GetUserFunction2("logbase"); |
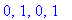
La procédure
Tokenize (
expr :: string ) va
supprimer les espaces " " puis découper l'expression
expr en éléments appelés
tokens en
précisant leur type.
Exemple :
[number,"6",6] , [unaryoperator,"+-"], [closepar,")"], [function1,"ln"] ...
Le parenthésage est vérifié par
l'intermédiaire de la variable
level
.
|
> |
Tokenize:=proc(expr::string)
global indx,st;
local ret,hasleftopd,level,s,ch,nb,id,f;
s:=RemoveChar(" ",expr):
if s="" then return [] end if;
ret:=NULL: indx:=0: level:=0: st:=stack[new]():
hasleftopd:=false;
while indx<length(s) do
indx:=indx+1: ch:=s[indx]:
if IsDigit(ch) then ret:=ret,[`number`,GetNumber(s,indx)]:
hasleftopd:=true
elif IsAlpha(ch) then
id:=GetIdentifier(s,indx): hasleftopd:=true:
f:=GetFunction1(id):
if f>0 then ret:=ret,[`function1`,id]
else
f:=GetFunction2(id):
if f>0 then ret:=ret,[`function2`,id] else
f:=GetUserFunction1(id):
if f>0 then ret:=ret,[`userfunction1`,id] else
f:=GetUserFunction2(id):
if f>0 then ret:=ret,[`userfunction2`,id] else
ret:=ret,[`identif`,id] end if;
end if
end if
end if
elif ch="(" then
hasleftopd:=false: level:=level+1: ret:=ret,[`openpar`,"("]
elif ch=")" then
hasleftopd:=true: level:=level-1: ret:=ret,[`closepar`,")"]
elif ch="," then
hasleftopd:=false: ret:=ret,[`comma`,","]
elif ch="+" then
if hasleftopd then ret:=ret,[`binaryoperator`,"+"] end if
elif ch="-" then
if hasleftopd then ret:=ret,[`binaryoperator`,"-"] else
ret:=ret,[`unaryoperator`,"+-"] end if
elif member(ch,Operators minus {"+","-","+-"},'f') then
ret:=ret,[`binaryoperator`,ch]
else ret:=ret,[`error`,ch]
end if:
end do:
if level<>0 then error "parse error in expression" else [ret] end if
end proc:
|
![[]](images/npi24.gif)
|
> |
Tokenize("5147.28E-01-2*max(ln(8)+1 , 7 / 5)) /(3+2^6 ) ");
|
Error, (in Tokenize) parse error
in expression
|
> |
Tokenize("-9*(+2-ln((-6)/(-3)))");
|
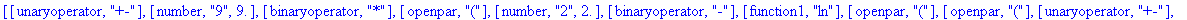

La procédure
toNPI (
expr :: string )
transforme l'expression expr
en NPI (notation polonaise inverse) après l'avoir
"tokenizée":
|
> |
toNPI:=proc(expr::string)
global Functions,UserFunctions;
local k,typ,tokens,ret,st,i,op1,op2;
ret:=NULL;
tokens:=Tokenize(expr):
if tokens=[] then error "nothing to do" end if;
st:=stack[new]();
for k to nops(tokens) do
typ:=tokens[k][1]:
if typ=`error` then error "syntax error in: " || tokens[k][2]
elif typ=`number` or typ=`identif` then ret:=ret,tokens[k]
elif
member(typ,{`function1`,`function2`,`userfunction1`,`userfunction2`}) then
stack[push](tokens[k],st)
elif typ=`openpar` then stack[push](tokens[k],st)
elif typ=`binaryoperator` then
op1:=tokens[k][2]:
if not stack[empty](st) and member(stack[top](st)[2],Operators,'i')
then
op2:=Operators[i]:
if (Assoc[op1]=left and Prec[op1]<=Prec[op2]) or (Assoc[op1]=right
and Prec[op1]<Prec[op2]) then
stack[pop](st):
if op2="+-" then ret:=ret,[`unaryoperator`,op2] else
ret:=ret,[`binaryoperator`,op2] end if;
end if
end if:
stack[push](tokens[k], st)
elif typ=`unaryoperator` and tokens[k][2]="+-" then
stack[push](tokens[k], st)
elif typ=`comma` then
while not stack[empty](st) and stack[top](st)[2]<>"(" do
ret:=ret,stack[top](st): stack[pop](st) end do;
stack[pop](st);
if stack[empty](st) then
error "empty stack: parse error"
end if
elif typ=`closepar` then
while not stack[empty](st) and stack[top](st)[2]<>"(" do
ret:=ret,stack[top](st): stack[pop](st) end do;
if not stack[empty](st) then stack[pop](st) end if;
if stack[empty](st) then #print( "empty stack")
else
if member(stack[top](st)[2],Functions union UserFunctions) then
ret:=ret,stack[top](st): stack[pop](st) end if:
if stack[empty](st) then error "empty stack: parse error" end if
end if
end if;
end do;
while not stack[empty](st) do ret:=ret,stack[top](st): stack[pop](st) end
do;
[ret]
end proc:
|
Error, (in toNPI) nothing to do
|
> |
s:="
(5-2*max(ln(8)+1 , 7 / 5)) /(3+2^6 ) "; toNPI(s);
|
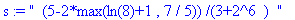

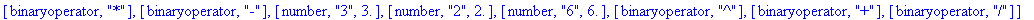
|
> |
s:=" +
logbase(10.25,6.12E3)/2 "; toNPI(s);
|
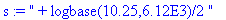
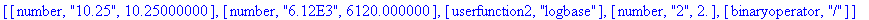
|
> |
s:="a+12*ln(b)+2*max(1e2,c)"; toNPI(s);
|
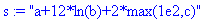

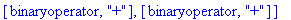
|
> |
s:="-9*(+2-ln((-6)/(-3)))"; toNPI(s);
|
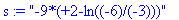

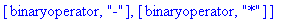
La procédure
NPIEvaluate (
s :: list) évalue à
partir de la liste obtenue à partir de la procédure précédente. On utilise une
pile ( stack en
anglais) dont les commandes sont:
- stack[new] : crée une nouvelle pile
vide.
- stack[push] : empile un élément au
sommet de la pile.
- stack[pop]: dépile, c'est à dire retire
un élément du sommet de la pile.
- stack[top]: donne l'élément situé sommet
de la pile.
- stack[empty]: teste si la pile est vide.
Description de l’algorithme
[source
wikipedia ]
tant qu’il y a des tokens à lire
:
lire le token.
si c’est un nombre l’ajouter à la sortie.
si c'est une fonction, le mettre sur la pile.
si c'est un séparateur d'arguments de fonction (par exemple une virgule) :
jusqu'à ce que l'élément au sommet de la pile soit une parenthèse
gauche, retirer l'élément du sommet
de la pile et l'ajouter à la sortie.
Si toute la pile est dépilée sans trouver de parenthèse gauche c’est
qu’il y a un mauvais parenthésage.
si c’est un opérateur o1 alors
1) s’il y a un opérateur o2 sur le haut de la pile et si l’une des
conditions suivantes est remplie.
o1 est associatif ou associatif à gauche et sa priorité est
inférieure ou égale à celle d’o2, ou
o1 est associatif à droit et sa priorité est inférieure à celle
d’o2,
retirer o2 de la pile pour le mettre dans la sortie
2) mettre o1 sur la pile
si le token est une parenthèse gauche, le mettre sur la pile.
si le token est une parenthèse droite, alors dépiler les opérateurs et les
mettant dans la sortie jusqu’à la parenthèse gauche
qui elle aussi sera dépilée, mais pas mise dans la sortie. Après cela, si le
token au sommet de la pile est une fonction, le dépiler
également pour l'ajouter à la sortie. Si toute la pile est dépilée sans
trouver de parenthèse gauche c’est qu’il y a un mauvais parenthésage.
Après la lecture du dernier token, s'il
reste des éléments dans la pile il faut tous les dépiler pour les mettre dans la
sortie
(il ne doit y avoir que des opérateurs:
si on trouve une parenthèse gauche c’est qu’il y a eu un mauvais parenthésage).
|
> |
NPIEvaluate:=proc(s::list)
global Functions1,Functions2,UserFunctions1,UserFunctions2;
local
typ,k,st,op,opd1,opd2,res,fn,Function1Evaluate,Function2Evaluate,UserFunction1Evaluate,UserFunction2Evaluate;
Function1Evaluate:=proc(f::string,opd)
local i,fn;
member(f,Functions1,'i'):
fn:=convert(Functions1[i],name):
fn(opd)
end proc:
Function2Evaluate:=proc(f::string,opd1,opd2)
local i,fn;
member(f,Functions2,'i'):
fn:=convert(Functions2[i],name):
fn(opd2,opd1)
end proc:
UserFunction1Evaluate:=proc(f::string,opd)
local i,fn;
member(f,UserFunctions1,'i'):
fn:=convert(UserFunctions1[i],name):
fn(opd)
end proc:
UserFunction2Evaluate:=proc(f::string,opd1,opd2)
local i,fn;
member(f,UserFunctions2,'i'):
fn:=convert(UserFunctions2[i],name):
fn(opd2,opd1)
end proc:
st:=stack[new]();
for k to nops(s) do
typ:=s[k][1]:
if typ=`unaryoperator` and s[k][2]="+-" then
opd1:=stack[top](st): stack[pop](st): stack[push](-opd1,st)
elif typ=`binaryoperator` then
opd1:=stack[top](st): stack[pop](st):
opd2:=stack[top](st): stack[pop](st):
op:=convert(s[k][2],name):
stack[push](op(opd2,opd1),st):
elif typ=`number` or typ=`identif` then stack[push](parse(s[k][2]),st)
elif typ=`function1` then
opd1:=stack[top](st): stack[pop](st):
stack[push](Function1Evaluate(s[k][2],opd1),st)
elif typ=`function2` then
opd1:=stack[top](st): stack[pop](st):
opd2:=stack[top](st): stack[pop](st):
stack[push](Function2Evaluate(s[k][2],opd1,opd2),st)
elif typ=`userfunction1` then
opd1:=stack[top](st): stack[pop](st):
stack[push](UserFunction1Evaluate(s[k][2],opd1),st)
elif typ=`userfunction2` then
opd1:=stack[top](st): stack[pop](st):
opd2:=stack[top](st): stack[pop](st):
stack[push](UserFunction2Evaluate(s[k][2],opd1,opd2),st)
else error "error in " || s[k][2]
end if
end do:
res:= stack[top](st): stack[pop](st):
res
end proc:
|
|
> |
s:="
(5-2*max(ln(a)+1 , 7 / 5)) /(3+2^6 ) "; : t:=toNPI(s): NPIEvaluate(t);
verif=parse(s); |
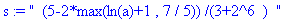
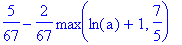
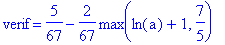
|
> |
s:="9-(5*(-3)+7)":
t:=toNPI(s): NPIEvaluate(t); verif=parse(s);
|
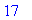
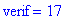
|
> |
s:="-9*(+2-ln((-6)/(-3)))": t:=toNPI(s): t:=NPIEvaluate(t); verif=parse(s);
evalf(t); |
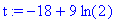
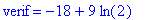
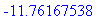
|
> |
s:="-sqrt(+max(-4+10,-14-54))"; t:=toNPI(s): NPIEvaluate(t); verif=parse(s);
|
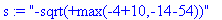
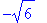

|
> |
s:="logbase(2,3)";
t:=toNPI(s): t:=NPIEvaluate(t); verif=parse("log[2](3)"); evalf(t);
|
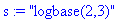
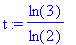
](images/npi51.gif)
©
- Alain Le Stang - Navigation optimisée pour une résolution 1024 x 768.
|
