|
Page d'accueil
Thèmes d'activités
<< Thème précédent
Thème suivant >>
Résolution d'un système linéaire par la méthode du pivot de Gauss:
>
with(linalg);
Warning, the protected names norm and trace have been redefined and unprotected
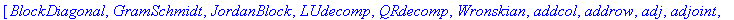

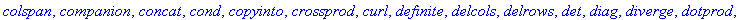
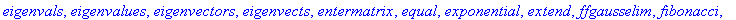
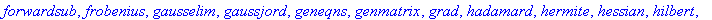

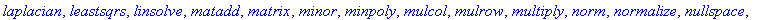
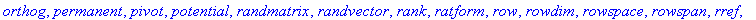
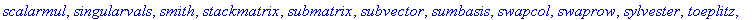
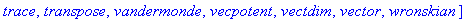
Question 1:
>
PermuteLignes:=proc(A::matrix,l1::posint,l2::posint)
print(`Echange des lignes`,L[l1],L[l2]); A:=swaprow(A,l1,l2);
end proc;
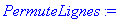
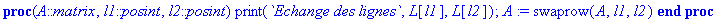
Question 2:
>
PermuteColonnes:=proc(A::matrix,c1::posint,c2::posint,T::array)
local temp;
temp:=T[c1];T[c1]:=T[c2];T[c2]:=temp;
print(`Echange des colonnes `,C[c1],C[c2]);
A:=swapcol(A,c1,c2);
end proc;
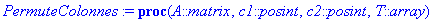
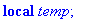
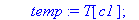
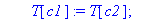
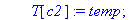
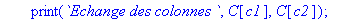
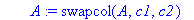

Question 3:
>
CherchePivotLigne:=proc(A::matrix,l1::posint,l2::posint,c::posint)
local i,ligne,maxi;
ligne:=0;maxi:=0;
for i from l1 to l2 do
if A[i,c]<>0 and abs(A[i,c])>maxi then
maxi:=abs(A[i,c]):ligne:=i
end if;
end do;
ligne;
end proc;
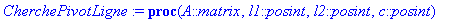

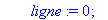
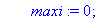
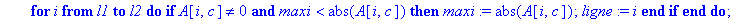

Question 4:
>
CherchePivotColonne:=proc(A::matrix,c1::posint,c2::posint,l::posint)
local j,colonne,maxi;
colonne:=0:maxi:=0:
for j from c1 to c2 do
if A[l,j]<>0 and
abs(A[l,j])>maxi then
maxi:=abs(A[l,j]);colonne:=j
end if;
end do;
colonne;
end proc;
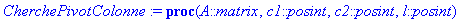
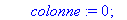
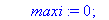
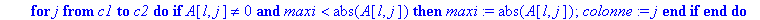

Question 5:
>
AfficheLigne:=proc(A::matrix,i::posint,T::array)
local j,p,X;
p:=coldim(A);
print(sum(A[i,j]*X[T[j]],j=1..p-1)=A[i,p])
end proc;
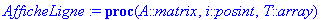

Question 6 a):
>
AfficheSolutions1:=proc(A::matrix,T::array)
local i,k,n,x,X,d;
n:=rowdim(A);
for i from n by -1 to 1 do
d:=0;
for k from 1+i to n do d:=d+A[i,k]*x[T[k]] end do;
x[T[i]]:=A[i,n+1]-d;
end do;
print(`Solution unique :`);
for i to n do print(X[T[i]]=x[T[i]]) end do;
end proc;

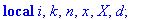
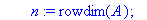
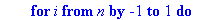
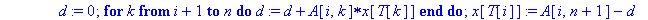


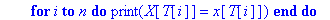

Question 6 b):
>
AfficheSolutions2:=proc(A::matrix,r::nonnegint,T::array)
local X,i,k,m,n,x,d;
m:=0;n:=rowdim(A);
for i from r+1 to n do
if A[i,r+1]<>0 then m:=m+1 end if;
end do;
if m>0 then print(`Pas de solution.`)
else
for i from r by -1 to 1 do
d:=0;
for k from 1+i to r do d:=d+A[i,k]*x[T[k]] end do;
x[T[i]]:=A[i,r+1]-d;
end do;
print(`Solution unique :`);
for i to r do print(X[T[i]]=x[T[i]]) end do;
end if;
end proc;
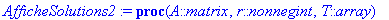
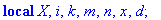
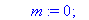
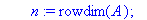
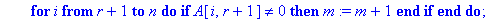



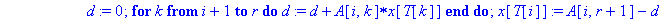

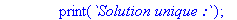
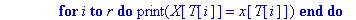


Question 6 c):
>
AfficheSolutions3:=proc(A::matrix,r::nonnegint,T::array)
local i,k,m,n,p,x,X,w,d,t,B;
n:=rowdim(A);p:=coldim(A)-1;
m:=0;
for i from r+1 to n do
if A[i,p+1]<>0 then m:=m+1 end if;
end do;
if m>0 then RETURN(`Pas de solution.`)
else
for i from r by -1 to 1 do
d:=0;
for k from 1+i to p do d:=d+A[i,k]*X[T[k]] end do;
X[T[i]]:=A[i,p+1]-d;
end do;
for k from 1 to r do
print(` X`[T[k]]=X[T[k]]);
end do;
for k from r+1 to p do
print(X[T[k]],` réel quelconque`)
end do;
end if;
end proc;
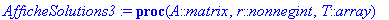
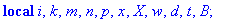
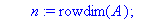
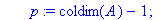
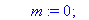
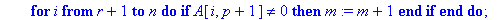



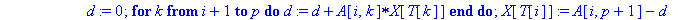

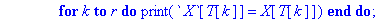
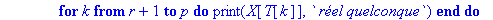


Question 7:
>
PivotGauss:=proc(A::matrix,rg)
local n,p,code,d,T,pivot,i,j,k,l,k1,k2,r;
n:=rowdim(A);p:=coldim(A)-1;
T:=array(1..p);
for i to p do T[i]:=i end do;
for i to n do AfficheLigne(A,i,T) end do;
print(`--------------------------------------`);
i:=0;r:=0;
while i<min(n,p) do
i:=i+1;
pivot:=A[i,i];
code:=NULL;
if pivot<>0 then
r:=r+1;
for k to p+1 do A[i,k]:=A[i,k]/pivot end do;
if pivot<>1 then
code:=code,L[i]=L[i]/pivot
end if;
for l from i+1 to n do
d:=A[l,i];
A:=addrow(A,i,l,-d);
if d<>0 then
code:=code,L[l]=L[l]-L[i]*d/pivot end if;
end do;
for k to nops([code]) do
print(op(k,[code]))
end do;
print(` `);
for k to n do AfficheLigne(A,k,T) end do;
print(`--------------------------------------`);
else # si A[i,i]=0
k1:=CherchePivotLigne(A,i+1,n,i);
if k1>0 then
PermuteLignes(A,i,k1);i:=i-1;
else
k2:=CherchePivotColonne(A,i+1,p,i);
if k2>0 then
PermuteColonnes(A,i,k2,T);i:=i-1;
else
for j from p to i+1 by -1 do
k:=CherchePivotLigne(A,i+1,n,j);
if k>0 then
PermuteLignes(A,i,k);
PermuteColonnes(A,i,j,T);
i:=i-1;break;
end if;
end do;
end if;
end if;
end if;
end do;
rg:=r;
if r=n and r=p then AfficheSolutions1(A,T) end if;
if r=p and r<n then AfficheSolutions2(A,r,T) end if;
if r<p then AfficheSolutions3(A,r,T) end if;
end proc;

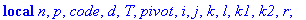
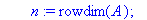
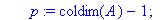

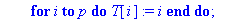


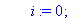
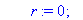
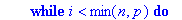
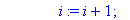
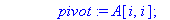
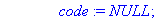
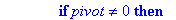
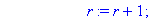
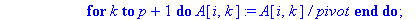
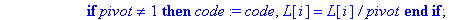
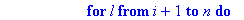
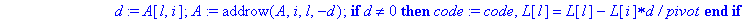

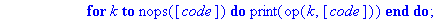
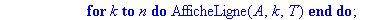







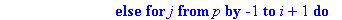

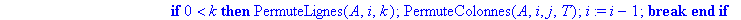





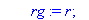
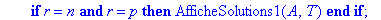

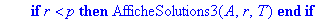

Question 8 a):
>
M:=matrix([[2,-1,3,9],[3,1,-1,7],[5,-2,1,5]]);
![M := matrix([[2, -1, 3, 9], [3, 1, -1, 7], [5, -2, ...](images/pivot122.gif)
>
PivotGauss(M,'r');print(`rang `=r);
![2*X[1]-X[2]+3*X[3] = 9](images/pivot123.gif)
![3*X[1]+X[2]-X[3] = 7](images/pivot124.gif)
![5*X[1]-2*X[2]+X[3] = 5](images/pivot125.gif)

![L[1] = 1/2*L[1]](images/pivot127.gif)
![L[2] = L[2]-3/2*L[1]](images/pivot128.gif)
![L[3] = L[3]-5/2*L[1]](images/pivot129.gif)

![X[1]-1/2*X[2]+3/2*X[3] = 9/2](images/pivot131.gif)
![5/2*X[2]-11/2*X[3] = -13/2](images/pivot132.gif)
![1/2*X[2]-13/2*X[3] = -35/2](images/pivot133.gif)

![L[2] = 2/5*L[2]](images/pivot135.gif)
![L[3] = L[3]-1/5*L[2]](images/pivot136.gif)

![X[1]-1/2*X[2]+3/2*X[3] = 9/2](images/pivot138.gif)
![X[2]-11/5*X[3] = -13/5](images/pivot139.gif)
![-27/5*X[3] = -81/5](images/pivot140.gif)

![L[3] = -5/27*L[3]](images/pivot142.gif)

![X[1]-1/2*X[2]+3/2*X[3] = 9/2](images/pivot144.gif)
![X[2]-11/5*X[3] = -13/5](images/pivot145.gif)
![X[3] = 3](images/pivot146.gif)

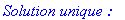
![X[1] = 2](images/pivot149.gif)
![X[2] = 4](images/pivot150.gif)
![X[3] = 3](images/pivot151.gif)
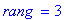
Question 8 b):
>
M:=matrix([[2,-1,1,5],[1,1,-2,-2],[4,1,-3,1]]);
![M := matrix([[2, -1, 1, 5], [1, 1, -2, -2], [4, 1, ...](images/pivot153.gif)
>
PivotGauss(M,'r');print(`rang `=r);
![2*X[1]-X[2]+X[3] = 5](images/pivot154.gif)
![X[1]+X[2]-2*X[3] = -2](images/pivot155.gif)
![4*X[1]+X[2]-3*X[3] = 1](images/pivot156.gif)

![L[1] = 1/2*L[1]](images/pivot158.gif)
![L[2] = L[2]-1/2*L[1]](images/pivot159.gif)
![L[3] = L[3]-2*L[1]](images/pivot160.gif)

![X[1]-1/2*X[2]+1/2*X[3] = 5/2](images/pivot162.gif)
![3/2*X[2]-5/2*X[3] = -9/2](images/pivot163.gif)
![3*X[2]-5*X[3] = -9](images/pivot164.gif)

![L[2] = 2/3*L[2]](images/pivot166.gif)
![L[3] = L[3]-2*L[2]](images/pivot167.gif)

![X[1]-1/2*X[2]+1/2*X[3] = 5/2](images/pivot169.gif)
![X[2]-5/3*X[3] = -3](images/pivot170.gif)
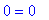

![` X`[1] = 1+1/3*X[3]](images/pivot173.gif)
![` X`[2] = -3+5/3*X[3]](images/pivot174.gif)
![X[3], ` réel quelconque`](images/pivot175.gif)
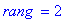
Question 8 c):
>
M:=matrix([[1,1,1,1,4,5],[1,-1,1,-1,0,-2],[2,0,2,1,5,4]]);
![M := matrix([[1, 1, 1, 1, 4, 5], [1, -1, 1, -1, 0, ...](images/pivot177.gif)
>
PivotGauss(M,'r');print(`rang `=r);
![X[1]+X[2]+X[3]+X[4]+4*X[5] = 5](images/pivot178.gif)
![X[1]-X[2]+X[3]-X[4] = -2](images/pivot179.gif)
![2*X[1]+2*X[3]+X[4]+5*X[5] = 4](images/pivot180.gif)

![L[2] = L[2]-L[1]](images/pivot182.gif)
![L[3] = L[3]-2*L[1]](images/pivot183.gif)

![X[1]+X[2]+X[3]+X[4]+4*X[5] = 5](images/pivot185.gif)
![-2*X[2]-2*X[4]-4*X[5] = -7](images/pivot186.gif)
![-2*X[2]-X[4]-3*X[5] = -6](images/pivot187.gif)

![L[2] = -1/2*L[2]](images/pivot189.gif)
![L[3] = L[3]-L[2]](images/pivot190.gif)

![X[1]+X[2]+X[3]+X[4]+4*X[5] = 5](images/pivot192.gif)
![X[2]+X[4]+2*X[5] = 7/2](images/pivot193.gif)
![X[4]+X[5] = 1](images/pivot194.gif)

![`Echange des colonnes `, C[3], C[4]](images/pivot196.gif)

![X[1]+X[2]+X[4]+X[3]+4*X[5] = 5](images/pivot198.gif)
![X[2]+X[4]+2*X[5] = 7/2](images/pivot199.gif)
![X[4]+X[5] = 1](images/pivot200.gif)

![` X`[1] = 3/2-2*X[5]-X[3]](images/pivot202.gif)
![` X`[2] = 5/2-X[5]](images/pivot203.gif)
![` X`[4] = 1-X[5]](images/pivot204.gif)
![X[3], ` réel quelconque`](images/pivot205.gif)
![X[5], ` réel quelconque`](images/pivot206.gif)
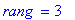
|

![M := matrix([[2, -1, 3, 9], [3, 1, -1, 7], [5, -2, ...](images/pivot122.gif)
![M := matrix([[2, -1, 1, 5], [1, 1, -2, -2], [4, 1, ...](images/pivot153.gif)
![M := matrix([[1, 1, 1, 1, 4, 5], [1, -1, 1, -1, 0, ...](images/pivot177.gif)